[PRML] Chapter 1. Introduction (4) - 정보 이론

본 글은 책 ‘패턴 인식과 머신 러닝’의 국내 출판본을 바탕으로 작성되었습니다.

1.6 정보 이론

정보량과 엔트로피

변수 $x$가 특정 값을 가지고 있는 것을 확인했을 때 전해지는 정보량은 얼마일까요? 매우 일어날 가능성이 높은 사건이 일어났다는 사실을 들었을 때보다 일어나기 힘든 사건이 발생했다는 사실을 들었을 때 더 많은 정보를 전달받게 됩니다. 따라서 정보량의 측정 단위는 확률 분포 $p(x)$에 종속적이게 됩니다. 지금부터 정보량을 표현하는 함수 $h(x)$를 알아보도록 하겠습니다.

서로 연관되어 있지 않은 사건 $x$와 $y$가 있습니다. 이 경우 두 사건이 함께 일어났을 때 얻는 정보량은 각자의 사건이 따로 일어났을 때 얻는 정보량의 합이 됩니다. 따라서 $h(x,y) = h(x) + h(y)$ 입니다. 독립인 사건 $x, y$에 대해 $p(x, y) = p(x)p(y)$ 이므로 $h(x)$는 $p(x)$의 로그에 해당합니다.

\[h(x) = -\log_2p(x)\]

음의 부호는 정보량이 음의 값을 가지지 않게 하기 위해 붙였습니다. 사건 $x$의 확률이 낮을수록 얻을 수 있는 정보량은 큽니다. 어떤 확률 변수 값의 정보량의 평균치는 $p(x)$에 대해 위 식의 기댓값을 구함으로써 알아낼 수 있습니다.

\[H[x] = -\sum_xp(x)\log_2p(x)\]

이 값이 바로 확률 변수 $x$의 엔트로피 입니다. $p(x) = 0$인 $x$값에 대해서는 $p(x)\log_2p(x)=0$ 입니다. 식에 따라서 비균일 분포의 엔트로피가 균일 분포의 엔트로피보다 낮다는 것을 알 수 있습니다. 엔트로피는 보통 무질서의 척도로서 해석됩니다. 또한 확률 변수의 상태를 결정짓는 데 필요한 정보량의 평균이라고 정의할 수 있습니다.

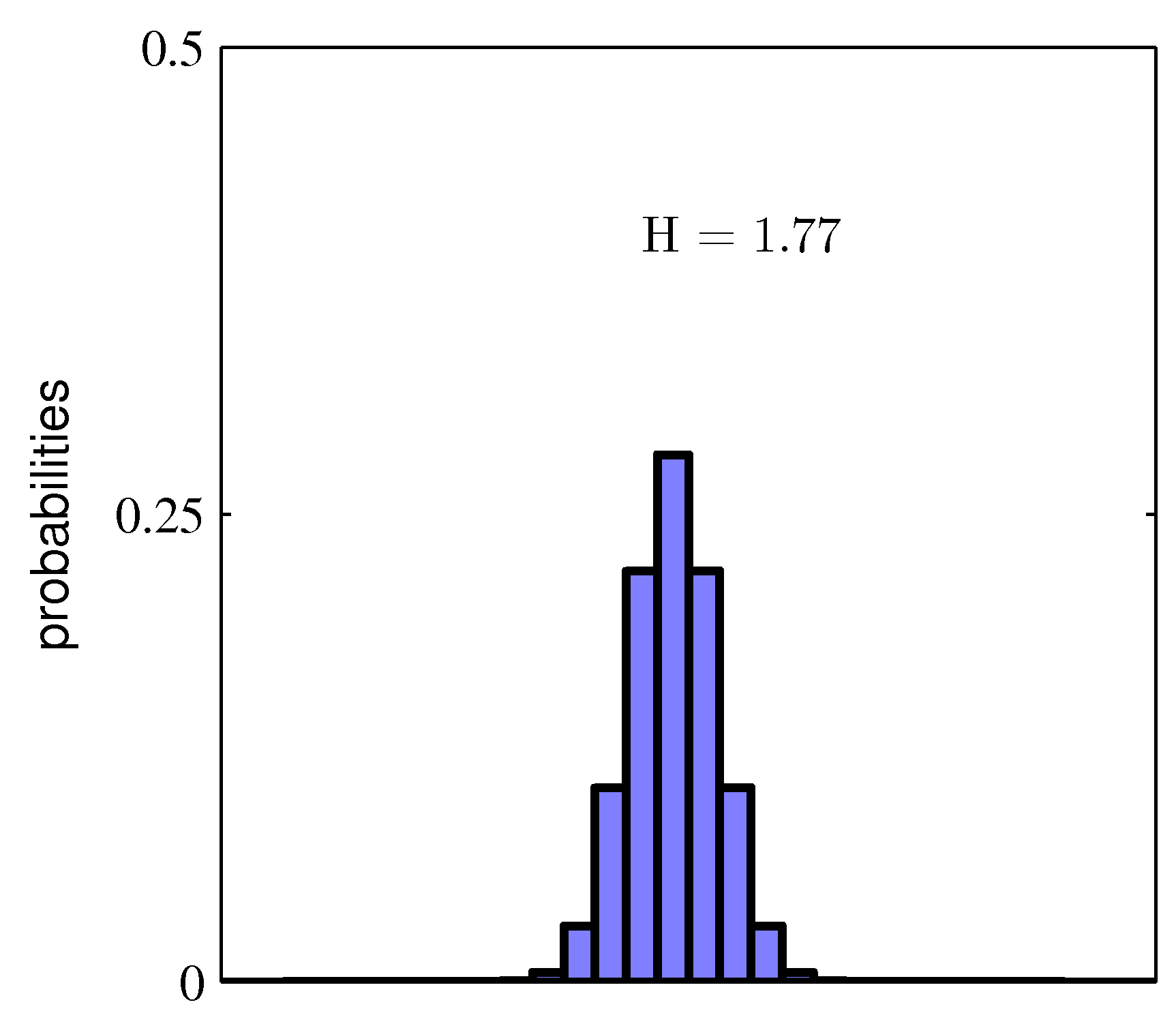
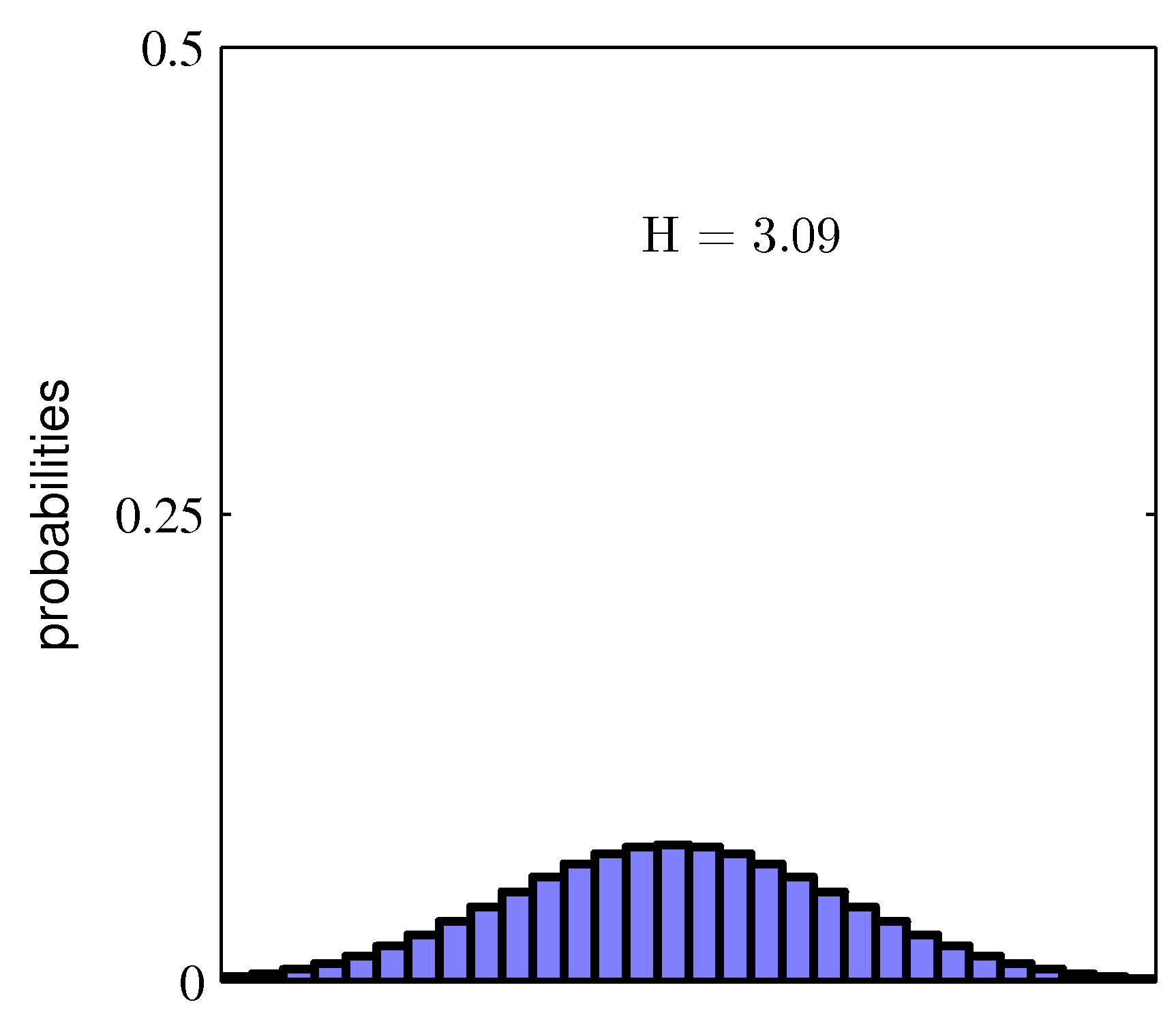
Figure 1.30 두 확률 분포의 히스토그램

위 그림을 보면 분포 $p(x_i)$가 몇몇 값에 뾰족하게 집중되어 있는 경우 상대적으로 낮은 엔트로피를 가지는 반면, 많은 값들 사이에 퍼져 있을 때는 높은 엔트로피를 가집니다. 엔트로피가 최대가 되는 경우는 랑그랑주 승수법을 활용하여 $\text{H}$의 최댓값을 찾아냄으로써 알아낼 수 있습니다. $\text{H}$에 확률의 정규화 제약 조건을 포함시키면 다음 식이 됩니다.

\[\widetilde{\text{H}} = -\sum_ip(x_i)\ln p(x_i)+\lambda \left(\sum_ip(x_i)-1\right)\]

위 식이 최대화되는 경우는 모든 $p(x_i)$ 값이 같은 경우라는 것을 알 수 있습니다. 이 경우 $x_i$의 상태 가짓수가 $M$ 이라면 해당 엔트로피 값은 $\text{H} = \ln M$ 입니다.

연속 변수의 엔트로피

이제 연속 변수 $x$에 대한 분포 $p(x)$를 포함시켜 보겠습니다. 첫 번째로 $x$를 너비 $\Delta$의 여러 구간으로 나누겠습니다. $p(x)$가 연속적이라고 가정할 경우 평균값의 정리에 따라 각각의 구간에는 다음을 만족시키는 $x_i$ 값이 존재합니다.

\[\int^{(i+1)\Delta}_{i\Delta}p(x)dx = p(x_i)\Delta\]

이제 모든 $x$값에 대해서 해당 값이 $i$번째 칸에 속할 경우에 값 $x_i$를 할당해 보겠습니다. 이 과정을 통해 연속적인 변수 $x$를 정량화하게 됩니다. 이 경우 $x_i$를 관측하게 될 확률은 $p(x_i)\Delta$가 됩니다.

\[\text{H}_\Delta = - \sum_ip(x_i)\Delta\ln(p(x_i)\Delta) = -\sum_ip(x_i)\Delta\ln p(x_i)-\ln\Delta\]

아까 활용한 평균값의 정리에 따라 $\sum_ip(x_i)\Delta = 1$ 이라는 사실을 사용했습니다. 이제 위 식의 오른쪽 변 두번째 항인 $-\ln\Delta$를 제외하고 $\Delta\rightarrow0$을 고려해 보겠습니다.

\[\lim_{\Delta\rightarrow0}\left\{-\sum_ip(x_i)\Delta\ln p(x_i)\right\} = -\int p(x)\ln p(x)dx\]

위 식의 오른쪽 변을 미분 엔트로피 라고 합니다. $\Delta\rightarrow0$을 취할 경우 $\ln\Delta$ 값은 발산하므로 연속 변수의 엔트로피를 정확하게 지정하기 위해서는 아주 많은 수의 비트가 필요함을 알 수 있습니다. 벡터 $\mathbf{x}$에 대해 정의된 밀도의 경우 다음과 같이 나타낼 수 있습니다.

\[\text{H}[\mathbf{x}] = -\int p(\mathbf{x})\ln p(\mathbf{x})d\mathbf{x}\]

조건부 엔트로피

$\mathbf{x}$값과 $\mathbf{y}$값을 함께 뽑는 결합 분포 $p(\mathbf{x},\mathbf{y})$에 대해 고려해 보겠습니다. $\mathbf{x}$의 값이 알려져 있다면 그에 해당하는 $\mathbf{y}$값을 알기 위해 필요한 정보는 $-\ln p(\mathbf{y}\vert\mathbf{x})$ 입니다. 따라서 $\mathbf{y}$를 특정하기 위해 추가로 필요한 정보의 평균값은 다음과 같습니다.

\[\text{H}[\mathbf{y}\vert\mathbf{x}] = -\int\int p(\mathbf{y}, \mathbf{x})\ln p(\mathbf{y}\vert\mathbf{x})d\mathbf{y}d\mathbf{x}\]

이를 $\mathbf{x}$의 $\mathbf{y}$에 대한 조건부 엔트로피라 합니다. 확률의 곱 법칙을 적용하면 다음을 도출해 낼 수 있습니다.

\[\text{H}[\mathbf{x},\mathbf{y}] = \text{H}[\mathbf{y}\vert\mathbf{x}] + \text{H}[\mathbf{x}]\]

위 식에 의해 $\mathbf{x}$와 $\mathbf{y}$를 특정짓기 위해 필요한 정보의 양은 $\mathbf{x}$만 따로 특정짓기 위해 필요한 정보의 양과, $\mathbf{x}$가 주어졌을 때 $\mathbf{y}$를 특정짓기 위해 필요한 정보의 양을 합한 것과 같습니다.

상대적 엔트로피와 상호 정보량

알려지지 않은 분포 $p(\mathbf{x})$를 피팅하기 위해 모델을 만들었으며 그 결과로 분포 $q(\mathbf{x})$를 구했다고 해보겠습니다. 만약 $q(\mathbf{x})$를 이용하여 $\mathbf{x}$의 값을 전달하기 위해 코드를 만든다고 하면 $p(\mathbf{x})$가 아닌 $q(\mathbf{x})$를 사용했으므로 추가 정보가 필요합니다. 이때 추가로 필요한 정보의 양은 다음과 같이 주어집니다.

\[\begin{aligned}\text{KL}(p\Vert q) &= -\int p(\mathbf{x})\ln q(\mathbf{x})d\mathbf{x} -\left(-\int p(\mathbf{x})\ln p(\mathbf{x})d\mathbf{x}\right)\\&=-\int p(\mathbf{x})\ln\left\{\frac{q(\mathbf{x})}{p(\mathbf{x})}\right\}\end{aligned}\]

위 식을 $p(\mathbf{x})$와 $q(\mathbf{x})$ 간의 상대 엔트로피 혹은 쿨백 라이블러 발산 KL divergence 라고 부릅니다. 이 식은 대칭적이지 않으며 따라서 $\text{KL}(p\Vert q) \ne \text{KL}(q\Vert p)$ 입니다. 이제 $\text{KL}(p\Vert q) = 0$ 일 때, $p(\mathbf{x}) = q(\mathbf{x})$임을 증명해보겠습니다.

증명

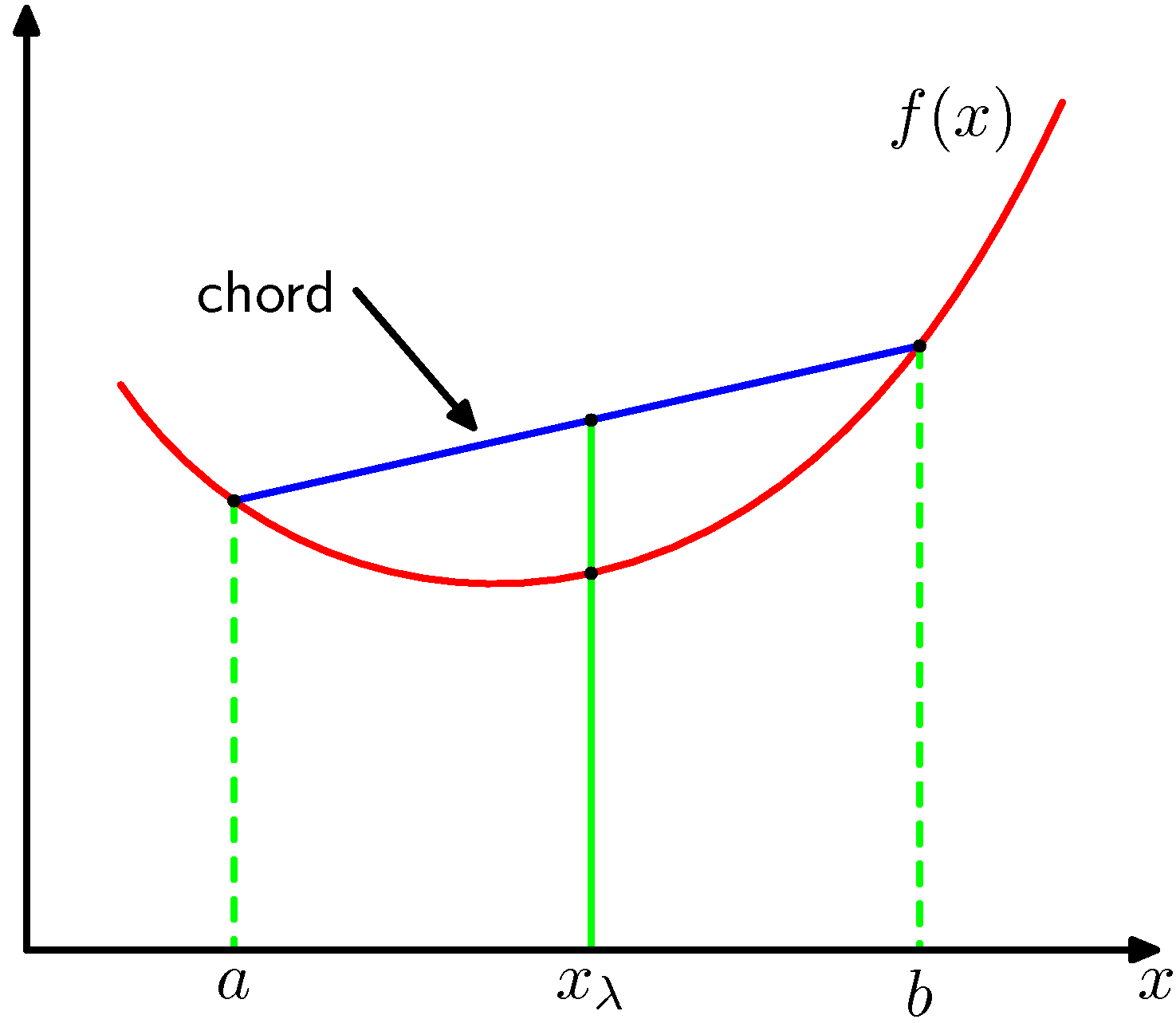Figure 1.31 볼록 함수

우선 볼록 함수에 대해 살펴보겠습니다. 위 그림과 같이 모든 현이 함수상에 혹은 그 위에 존재하는 경우 함수 $f(x)$가 볼록하다고 말합니다. 이때 $x=a$에서 $x=b$ 사이 구간의 $x$ 값은 $0 \leq \lambda \leq 1$인 경우에 $\lambda a + (1 - \lambda)b$ 라고 적을 수 있습니다. 이 구간에 해당하는 현은 $\lambda f(a) + (1-\lambda)f(b)$가 되며 해당 구간의 함수값은 $f(\lambda a + (1-\lambda)b)$ 입니다. 이 경우 함수의 볼록성은 다음 식으로 설명합니다.

\[f(\lambda a + (1-\lambda)b) \leq \lambda f(a) + (1 - \lambda)f(b)\]

이는 함수의 이차 미분값이 모든 구간에서 양의 값을 가진다는 것과 동일합니다. 수학적 귀납법을 사용하면 위 식으로부터 볼록 함수 $f(x)$가 다음을 만족함을 증명할 수 있습니다.

\[f\left(\sum^M_{i=1}\lambda_ix_i\right) \leq \sum^ M_{i=1}\lambda_if(x_i)\]

여기서 모든 포인트들의 집합 ${x_i}$에 대해서 $\lambda_i \geq 0$이며, $\sum_i \lambda_i = 1$ 입니다. 위 식을 옌센의 부등식 이라고 합니다. $\lambda_i$를 ${x_i}$를 값으로 가지는 이산 변수 $x$상의 확률 분포라고 해석하면 위 식을 다음과 같이 적을 수 있습니다.

\[f(\mathbb{E}[x]) \leq \mathbb{E}[f(x)]\]

연속 변수에 대해서 옌센의 부등식은 다음 형태를 취하게 됩니다.

\[f\left(\int\mathbf{x}p(\mathbf{x})d\mathbf{x}\right) \leq \int f(\mathbf{x})p(\mathbf{x})d\mathbf{x}\]

위 형태의 옌센의 부등식을 쿨백 라이블러 발산에 적용하면 다음을 얻습니다.

\[\text{KL}(p\Vert q) = -\int p(\mathbf{x})\ln\left\{\frac{q(\mathbf{x})}{p(\mathbf{x})}\right\}d\mathbf{x} \geq -\ln\int q(\mathbf{x})d\mathbf{x} = 0\]

여기서는 $-\ln x$가 볼록 함수라는 사실과 $\int q(\mathbf{x})d\mathbf{x} = 1$이라는 사실이 사용되었습니다. $-\ln x$가 순볼록 함수고 등식이 성립하는 것은 모든 $x$에 대하여 $q(\mathbf{x}) = p(\mathbf{x})$인 것의 필요 충분 조건이 됩니다. 따라서 두 분포 $p(\mathbf{x})$와 $q(\mathbf{x})$가 얼마나 다른지의 척도로 쿨백 라이블러 발산을 사용할 수 있습니다.

우리가 모델링하고자 하는 알려지지 않은 분포 $p(\mathbf{x})$로부터 데이터가 만들어지는 상황을 가정하겠습니다. 변경 가능한 매개변수 $\theta$에 대해 종속적인 매개변수 분포 $q(\mathbf{x}\vert\theta)$를 이용해서 분포 $p(\mathbf{x})$를 추정하고자 할 수 있습니다. $\theta$를 구하는 한 가지 방법은 $p(\mathbf{x})$와 $q(\mathbf{x}\vert\theta)$ 사이의 쿨백 라이블러 발산을 최소화하는 $\theta$를 찾는 것입니다. $p(\mathbf{x})$에 대해 정확히 알고 있지 못하므로 직접적으로 계산하는 것은 불가능합니다. 하지만 $p(\mathbf{x})$에서 유한한 숫자의 훈련 집합 $\mathbf{x}_n(n = 1, …, N)$ 을 추출했다고 가정해 보겠습니다.

\[\text{KL}(p\Vert q) \simeq \frac1N\sum^N_{n=1}\{-\ln q(\mathbf{x}_n\vert\theta)+\ln p(\mathbf{x}_n)\}\]

이와 같이 유한한 합으로 $p(\mathbf{x})$에 대한 기댓값을 근사할 수 있습니다. 위 식의 오른쪽 변의 두 번째 항은 $\theta$로부터 독립적입니다. 그리고 첫번째 항은 분포 $q(\mathbf{x}\vert\theta)$ 하에서의 $\theta$의 음의 로그 가능도 함수를 훈련 집합을 이용해서 계산한 것입니다. 따라서 쿨백 라이블러 발산을 최소화하는 것은 가능도 함수를 최대화하는 것과 같습니다.

\[\begin{aligned} \text{I}[\mathbf{x},\mathbf{y}]&\equiv\text{KL}(p(\mathbf{x},\mathbf{y})\Vert p(\mathbf{x})p(\mathbf{y})) \\ &= -\int\int p(\mathbf{x}, \mathbf{y})\ln\left(\frac{p(\mathbf{x})p(\mathbf{y})}{p(\mathbf{x},\mathbf{y})}\right)d\mathbf{x}d\mathbf{y}\end{aligned}\]

위 식은 결합 분포 $p(\mathbf{x},\mathbf{y})$에 대해 살펴본 것입니다. 두 변수 집합이 독립적이지 않다면 결합 분포와 주변 분포 간 곱 사이의 쿨백 라이블러 발산을 이용하여 변수들이 얼마나 독립적인지 알아볼 수 있습니다.

위 식을 변수 $\mathbf{x}$와 $\mathbf{y}$ 사이의 상호 정보량 mutual information 이라고 합니다. 쿨백 라이블러 발산의 성질에 따라 $\text{I}[\mathbf{x},\mathbf{y}] \geq 0$ 이며, $\mathbf{x}$와 $\mathbf{y}$가 독립적일 때만 $\text{I}[\mathbf{x},\mathbf{y}] = 0$ 입니다. 또한 상호 정보량은 조건부 엔트로피와 다음의 관계가 있습니다.

\[\text{I}[\mathbf{x},\mathbf{y}] = \text{H}[\mathbf{x}] - \text{H}[\mathbf{x}\vert\mathbf{y}] = \text{H}[\mathbf{y}] - \text{H}[\mathbf{y}\vert\mathbf{x}]\]

베이지안 관점에서는 $p(\mathbf{x})$를 $\mathbf{x}$에 대한 사전 분포로, $p(\mathbf{x}\vert\mathbf{y})$를 새로운 데이터 $\mathbf{y}$를 관찰한 후의 사후 분포로 볼 수 있습니다. 따라서 상호 정보량은 새 관찰값 $\mathbf{y}$의 결과로 줄어드는 $\mathbf{x}$에 대한 불확실성을 표현한 것이 됩니다.