[PRML] Chapter 2. Probability Distribution (2) - 다항 변수

본 글은 책 ‘패턴 인식과 머신 러닝’의 국내 출판본을 바탕으로 작성되었습니다.

2.2 다항 변수

다항 분포

전 글에서 살펴본 이산 확률 변수는 두 가지 가능한 값들 중 하나를 취하는 수량을 설명하는 데 사용됩니다. 따라서 2개보다 더 많은 $K$개의 값이 있다면 이 중 하나를 취할 수 있는 이산 변수를 활용해야 합니다. 이런 변수를 표현하기 위해 원 핫 인코딩 one hot encoding 이 사용됩니다. 각각의 변수가 $K$차원의 벡터 $\mathbf{x}$로 나타내지며 $x_k$값들 중 하나는 1, 나머지 값들은 0으로 표현됩니다. 이러한 벡터들은 $\sum^K_{k_1}x_k=1$이라는 성질을 만족합니다. 만약 우리가 $x_k = 1$ 이 될 확률을 $\mu_k$라고 한다면 $\mathbf{x}$의 분포는 다음과 같습니다.

\[p(\mathbf{x}\vert\mu) = \prod^K_{k=1}\boldsymbol{\mu}_k^{x_k}\]

여기서 $\boldsymbol{\mu} = (\mu_1, …, \mu_K)^\text{T}$ 이며 $\mu_k$는 확률을 표현하고 있기 때문에 $\mu_k \geq 0$과 $\sum_k\mu_k = 1$을 만족합니다. 위 식은 베르누이 분포를 결괏값이 두 가지 이상인 경우로 일반화한 것입니다. 이 분포에 대해서 다음 두 가지를 쉽게 증명할 수 있습니다.

\[\begin{aligned} \sum_\mathbf{x}p(\mathbf{x}\vert\boldsymbol{\mu})&=\sum^K_{k=1}\mu_k=1 \\ \mathbb{E}[\mathbf{x}\vert\boldsymbol{\mu}]=\sum_\mathbf{x}p(\mathbf{x}\vert\boldsymbol{\mu})\mathbf{x} &=(\mu_1, ..., \mu_K)^\text{T} = \boldsymbol{\mu} \end{aligned}\]

이제 $N$개의 독립적인 관측값 $\mathbf{x}_1, …, \mathbf{x}_N$을 가진 데이터 집합 $\mathcal{D}$을 고려해보겠습니다. 해당 가능도 함수는 다음의 형태를 지닙니다.

\[p(\mathcal{D}\vert\boldsymbol{\mu}) = \prod^K_{n=1}\prod^K_{k=1}\mu_k^{x_nk} = \prod^K_{k=1}\mu_k^{(\sum_nx_nk)} = \prod^K_{k=1}\mu_k^{m_k}\]

위 식에서 가능도 함숫값이 $K$값을 통해서만 $N$개의 데이터 포인트와 연관되어 있음을 확인할 수 있습니다.

\[m_k = \sum_nx_{nk}\]

위 식은 $x_k=1$인 관측값의 숫자에 해당하며, 이 분포의 충분 통계량 이라고 합니다.

이제 $\boldsymbol{\mu}$값의 최대 가능도 해를 찾기 위해서는 $\mu_k$의 합이 1이어야 한다는 제약 조건 하에서 $\ln p(\mathcal{D}\vert\boldsymbol{\mu})$의 최대값을 찾아야 합니다. 이를 위해서는 라그랑주 승수 $\lambda$를 사용해서 다음 식의 최댓값을 구하면 됩니다.

\[\sum^K_{k=1}m_k\ln\mu_k + \lambda\left(\sum^K_{k=1}\mu_k-1\right)\]

위 식을 $\mu_k$에 대해 미분한 뒤 이를 0으로 설정하면 다음이 구해집니다.

\[\mu_k = -m_k/\lambda\] \[\mu_k^{\text{ML}}=\frac{m_k}{N}\]

제약 조건 $\sum_k\mu_k=1$에 대입하면 라그랑주 승수 $\lambda = -N$임을 알 수 있습니다. 따라서 최대 가능도의 해는 위와 같은 형태를 띠게 되며, 이는 $N$개의 관측값 중 $x_k=1$인 경우의 비율입니다.

이제 매개변수 $\boldsymbol{\mu}$와 관측값의 숫자 $N$에 의해 결정되는 수량 $m_1, …, m_K$의 결합 분포를 고려해보겠습니다.

\[\text{Mult}(m_1, m_2, ..., m_K\vert\boldsymbol{\mu}, N) = {N \choose m_1m_2...m_K}\prod^K_{k=1}\mu_k^{m_k}\]

위 식이 바로 다항 분포 multinomial distribution 입니다. 정규화 계수는 $N$개의 물체를 각각 $m_1, …, m_K$의 수량을 가지는 $K$개의 집단으로 나누는 가짓수에 해당하며 다음과 같습니다. 여기서 변수 $m_K$는 제약 조건 $\sum^K_{k=1}m_k = N$을 가집니다.

\[{N \choose m_1m_2...m_k} = \frac{N!}{m_1!m_2!...m_K!}\]

디리클레 분포

이제 아까 살펴보았던 다항 분포의 매개변수 ${\mu_k}$들의 사전 분포에 대해 살펴보겠습니다. 다항 분포의 형태를 살펴보면 켤레 사전 분포는 다음과 같습니다.

\[p(\boldsymbol{\mu}\vert\boldsymbol{\alpha}) \propto \prod^K_{k=1}\mu_k^{\alpha_k-1}\]

여기서 ${0 \leq \mu_k \leq 1}$ 이며 $\sum_k\mu_k = 1$ 입니다. $\alpha_1, …, \alpha_K$들은 분포의 매개변수이며, $\boldsymbol{\alpha}$는 $(\alpha_1, …, \alpha_K)^\text{T}$를 지칭합니다. 합산 제약 조건 때문에 ${\mu_k}$에서의 이 분포는 $K - 1$차원의 단체simplex로 제약됩니다. $K=3$인 경우는 다음과 같습니다.

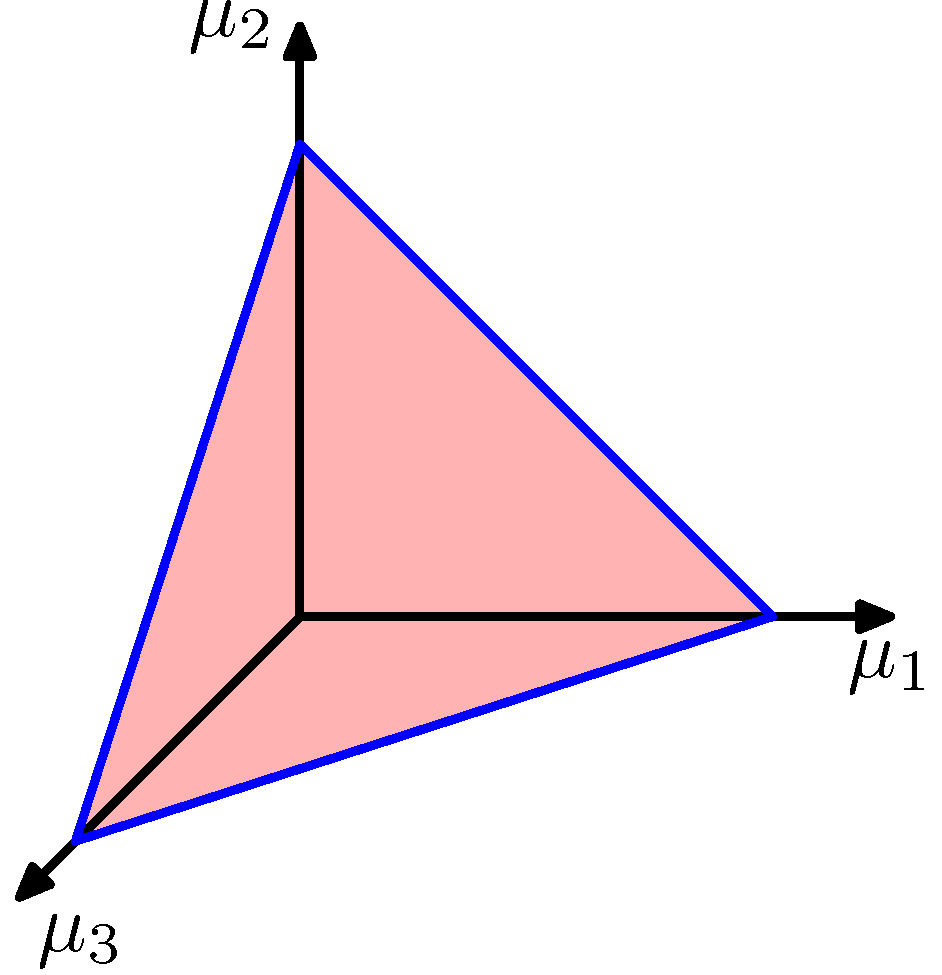Figure 2.4 세 개의 변수 $\mu_1, \mu_2, \mu_3$에 대한 디리클레 분포

이 분포의 정규화된 형태는 다음과 같습니다.

\[\text{Dir}(\boldsymbol{\mu}\vert\boldsymbol{\alpha}) = \frac{\Gamma(\alpha_0)}{\Gamma({\alpha_1})...\Gamma({\alpha_K})}\prod^K_{k=1}\mu_k^{\alpha_k-1}\]

위 식을 디리클레 분포 Dirichlet distribution 이라고 합니다. 여기서 $\alpha_0 = \sum^K_{k=1}\alpha_k$ 입니다. 다양한 매개변수 $\alpha_k$에 따른 단체상의 디리클레 분포 그래프는 다음과 같습니다.

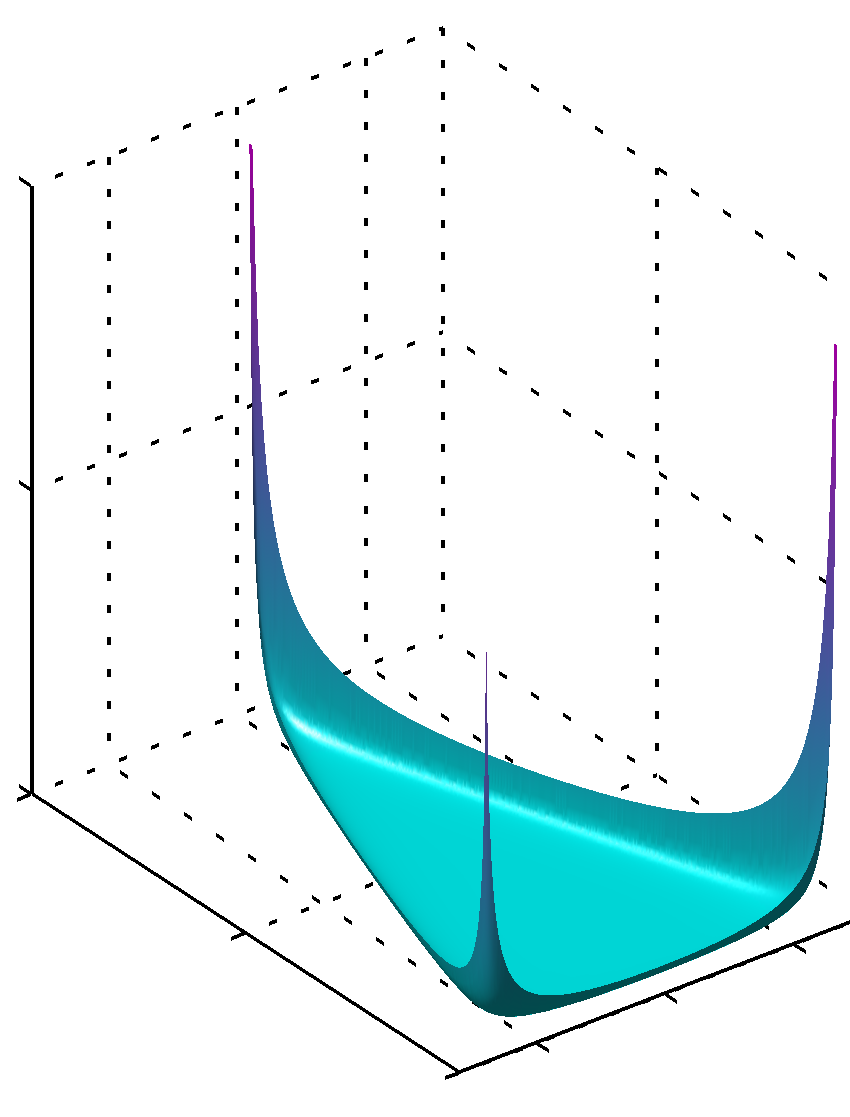
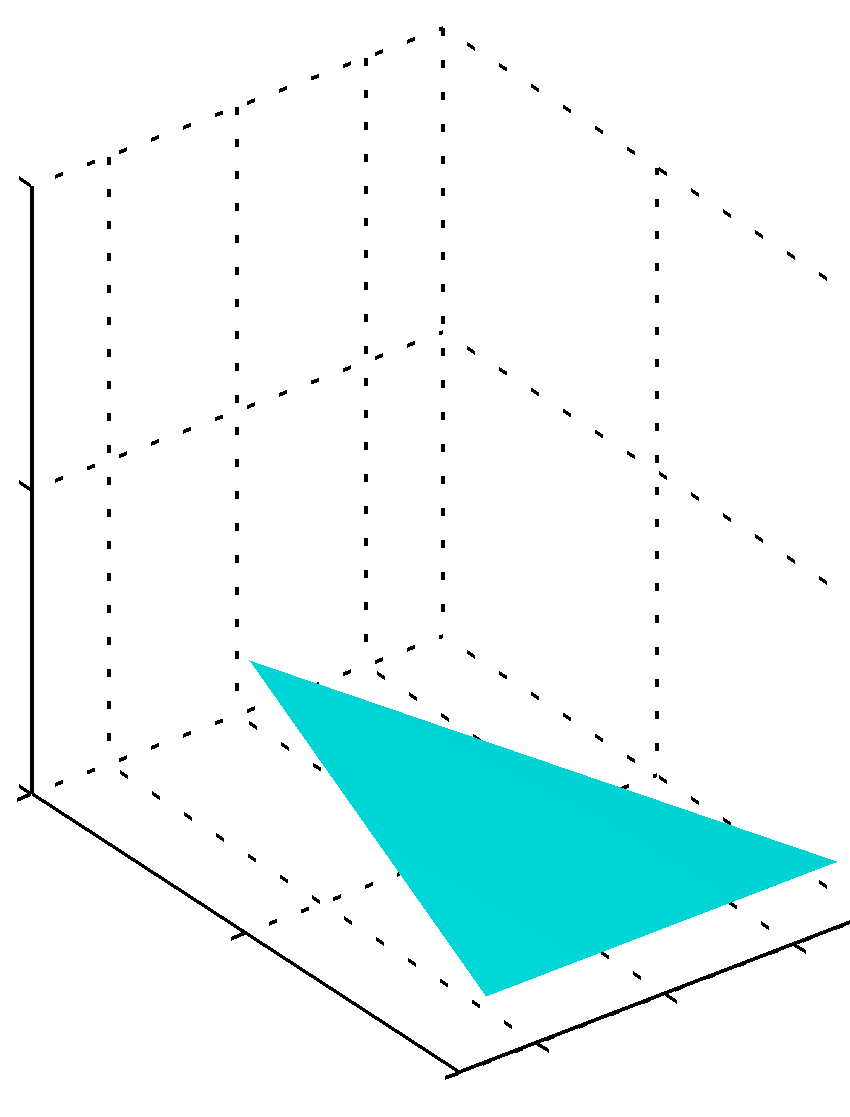
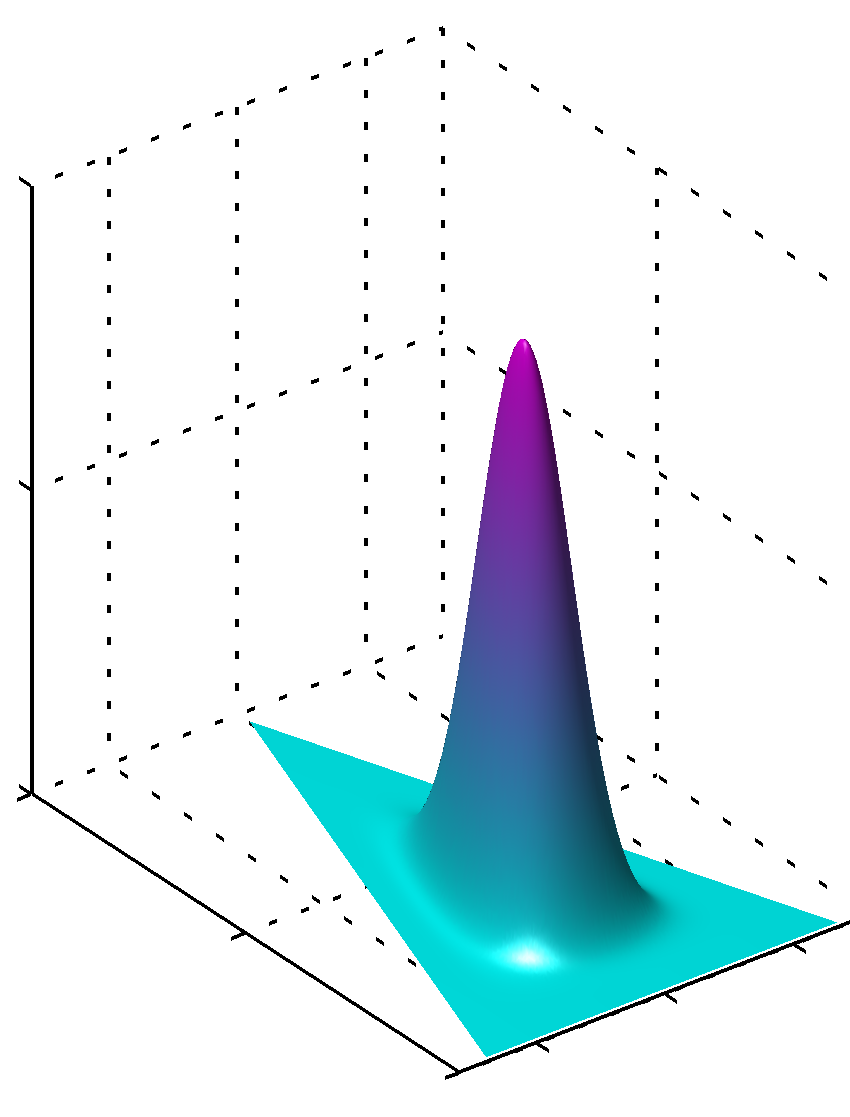
Figure 2.5 세 개의 변수에 대한 디리클레 분포. 각각 ${ \alpha_k = 0.1 }$, ${ \alpha_k = 1 }$, ${ \alpha_k = 10 }$ 이다.

위의 디리클레 분포식의 사전 분포에 다항 분포의 가능도 함수를 곱하면 ${ \mu_k }$의 사후 분포를 다음 형태로 구할 수 있습니다.

\[p(\boldsymbol{\mu}\vert\mathcal{D},\boldsymbol{\alpha}) \propto p(\mathcal{D}\vert\boldsymbol{\mu})p(\boldsymbol{\mu}\vert\boldsymbol{\alpha}) \propto \prod^K_{k=1}\mu_k^{\alpha_k+m_k-1}\]

사후 분포가 다시금 디리클레 분포의 형태를 띄게 됩니다. 따라서 디리클레 분포는 다항 분포의 켤레 사전 분포이며, 정규화 계수를 구할 수 있습니다.