[PRML] Chapter 2. Probability Distribution (3) - 가우시안 분포

본 글은 책 ‘패턴 인식과 머신 러닝’의 국내 출판본을 바탕으로 작성되었습니다.

2.3 가우시안 분포

가우시안 분포의 특징

식

단일 변수 $x$에 대한 가우시안 분포는 다음과 같습니다.

\[\mathcal{N}(x\vert\mu,\sigma^2) = \frac{1}{(2\pi\sigma^2)^\frac12}\exp\left\{-\frac1{2\sigma^2}(x-\mu)^2\right\}\]

여기서 $\mu$는 평균, $\sigma^2$는 분산입니다. $D$차원 벡터 $\mathbf{x}$에 대한 다변량 가우시안 분포는 다음과 같습니다.

\[\mathcal{N}(\mathbf{x}\vert\boldsymbol\mu, \boldsymbol{\Sigma}) = \frac1{(2\pi)^{D/2}}\frac1{\left\vert\boldsymbol{\Sigma}\right\vert^{1/2}}\exp\left\{-\frac12(\mathbf{x}-\boldsymbol{\mu})^\text{T}\boldsymbol{\Sigma}^{-1}(\mathbf{x}-\boldsymbol{\mu})\right\}\]

여기서 $\boldsymbol\mu$는 $D$차원 평균 벡터를, $\boldsymbol\Sigma$는 $D \times D$ 공분산 행렬을, $\left\vert\boldsymbol\Sigma\right\vert$는 $\boldsymbol\Sigma$의 행렬식을 의미합니다.

여러 확률 변수의 합에 대해 고려할 때 가우시안 분포를 사용할 수 있습니다. 중심 극한 정리 central limit theorem에 따르면 여러 개의 확률 변수들의 합에 해당하는 확률 변수는 몇몇 조건하에서 합해지는 확률 변수의 숫자가 증가함에 따라서 점점 가우시안 분포가 되어갑니다. 여기서 이항 분포 역시 $N \rightarrow \infty$이 됨에 따라 가우시안의 평태를 띈다는 점을 알 수 있습니다.

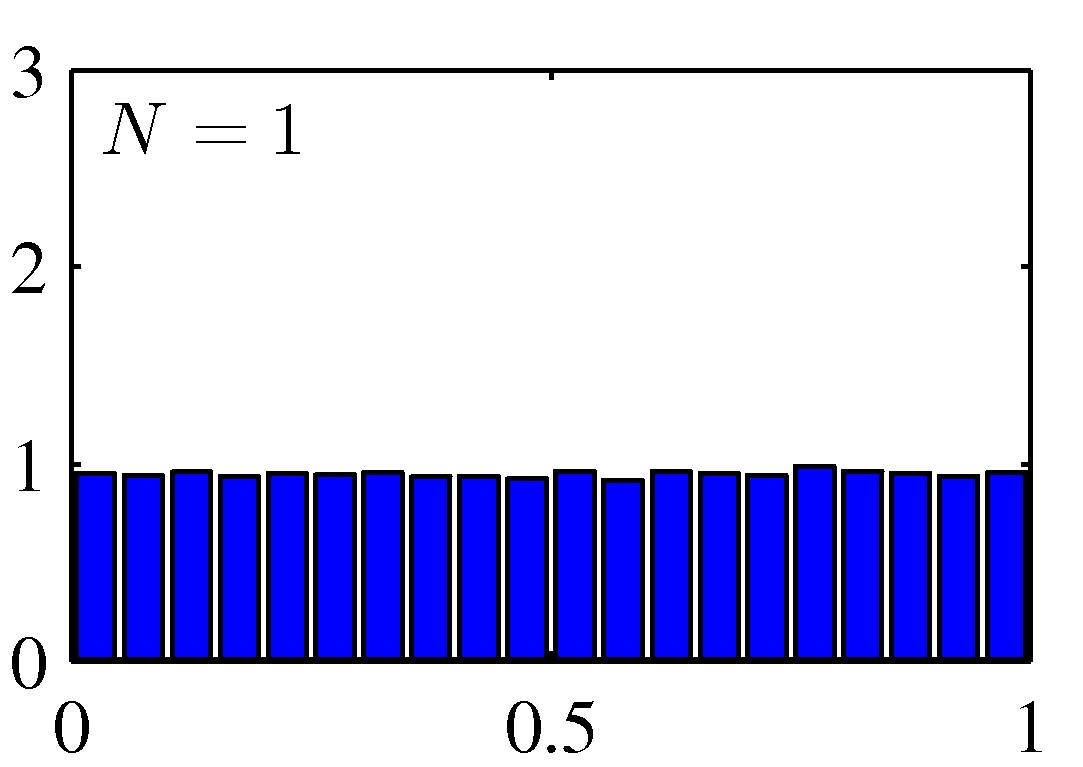
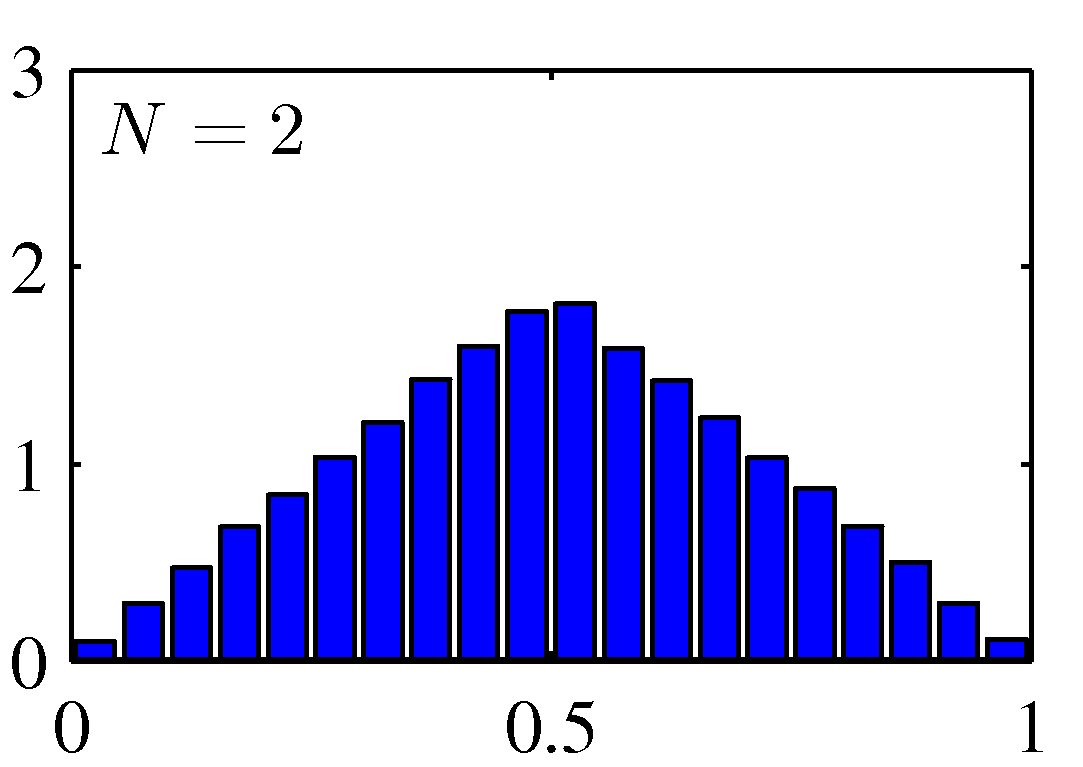
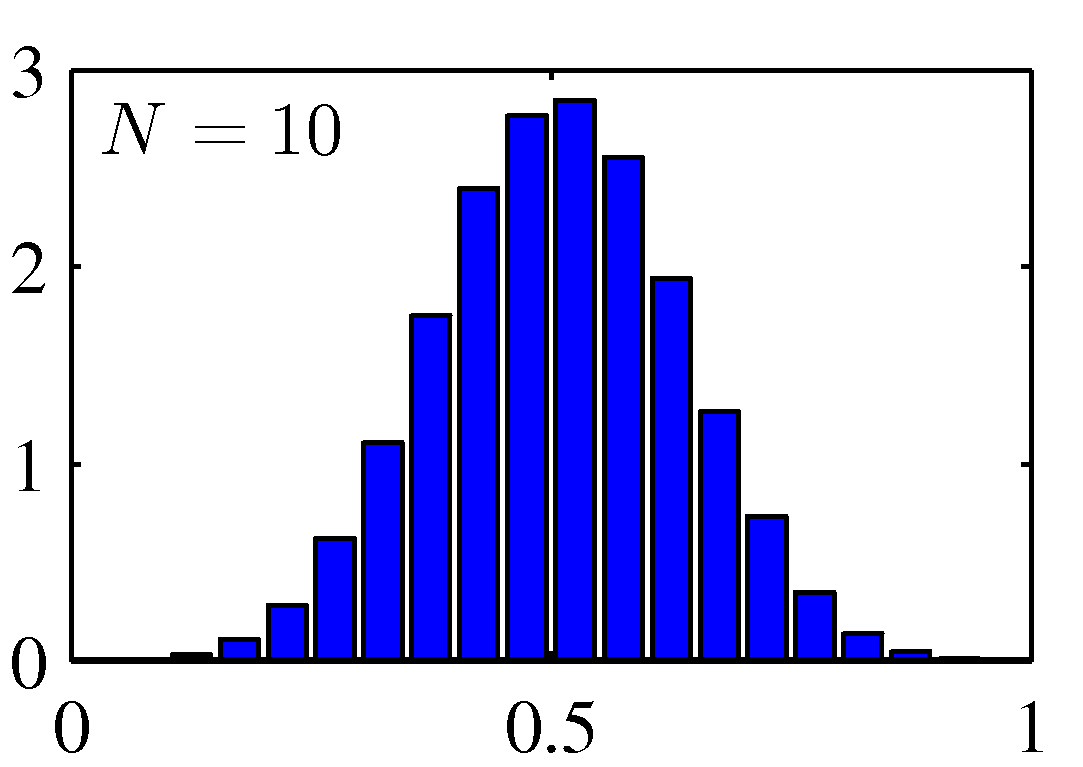
Figure 2.6 균일하게 분포된 $N$개의 값의 평균에 대한 히스토그램

기하학적 형태

$\mathbf{x}$에 대한 가우시안 분포의 함수적 종속성은 지수상에서 나타납니다. 이는 다음의 이차식 형태를 띱니다.

\[\Delta^2 = (\mathbf{x}-\boldsymbol\mu)^\text{T}\boldsymbol\Sigma^{-1}(\mathbf{x}-\boldsymbol\mu)\]

여기서 $\Delta$값은 $\boldsymbol\mu$로부터 $\mathbf{x}$까지의 마할라노비스 거리 Mahalanobis distance라고 합니다. 마할라노비스 거리는 $\boldsymbol\Sigma$가 항등 행렬일 경우 유클리디안 거리가 됩니다. 이 이차식이 상수가 되는 $\mathbf{x}$ 공간의 표면에서는 가우시안 분포 역시 상수가 됩니다. $\boldsymbol\Sigma$ 행렬은 비대칭 원소들이 지수로부터 사라지기 때문에 대칭성을 띱니다.

\[\boldsymbol\Sigma \mathbf{u}_i = \lambda_i\mathbf{u}_i\]

여기서 $i = 1, …, D$입니다. $\boldsymbol\Sigma$가 실수 대칭 행렬이므로 고윳값 역시 실수입니다. 정규직교 집합을 이루도록 고유 벡터들을 선택한다고 하겠습니다.

\[\mathbf{u}_i^\text{T}\mathbf{u}_j = I_{ij}\]

여기서 $I_{ij}$는 항등 행렬의 $i$와 $j$번째 원소입니다. 이때 고유 벡터를 이용해서 공분산 행렬 $\boldsymbol\Sigma$를 전개할 수 있으며 이는 다음 형태를 띱니다.

\[\begin{aligned} \boldsymbol\Sigma &= \sum^D_{i=1}\lambda_i\mathbf{u}_i\mathbf{u}_i^\text{T} \\ \boldsymbol\Sigma^{-1}&=\sum^D_{i=1}\frac1{\lambda_i}\mathbf{u}_i\mathbf{u}_i^\text{T} \end{aligned}\]

이 식을 위의 $\Delta^2$의 식에 대입하면 다음의 형태를 띱니다.

\[\begin{aligned} \Delta^2 = \sum^D_{i=1}\frac{y_i^2}{\lambda_i} \\ y_i = \mathbf{u}_i^\text{T}(\mathbf{x}-\boldsymbol{\mu}) \end{aligned}\]

${y_i}$를 정규직교 벡터 $\mathbf{u}_i$들로 정의되는 새로운 좌표계라고 해석할 수 있습니다. 원래의 $x_i$ 좌표계로부터 이동되고 회전된 것입니다. 벡터 $\mathbf{y} = (y_1,…,y_D)^\text{T}$이라 하면 다음과 같습니다.

\[\mathbf{y} = \mathbf{U(x-\boldsymbol\mu})\]

여기서 $\mathbf{U}$는 각각의 행이 $\mathbf{u}_i^\text{T}$로 주어지는 행렬입니다. $\mathbf{U}$는 직교 orthogonal한 행렬임을 알 수 있습니다.

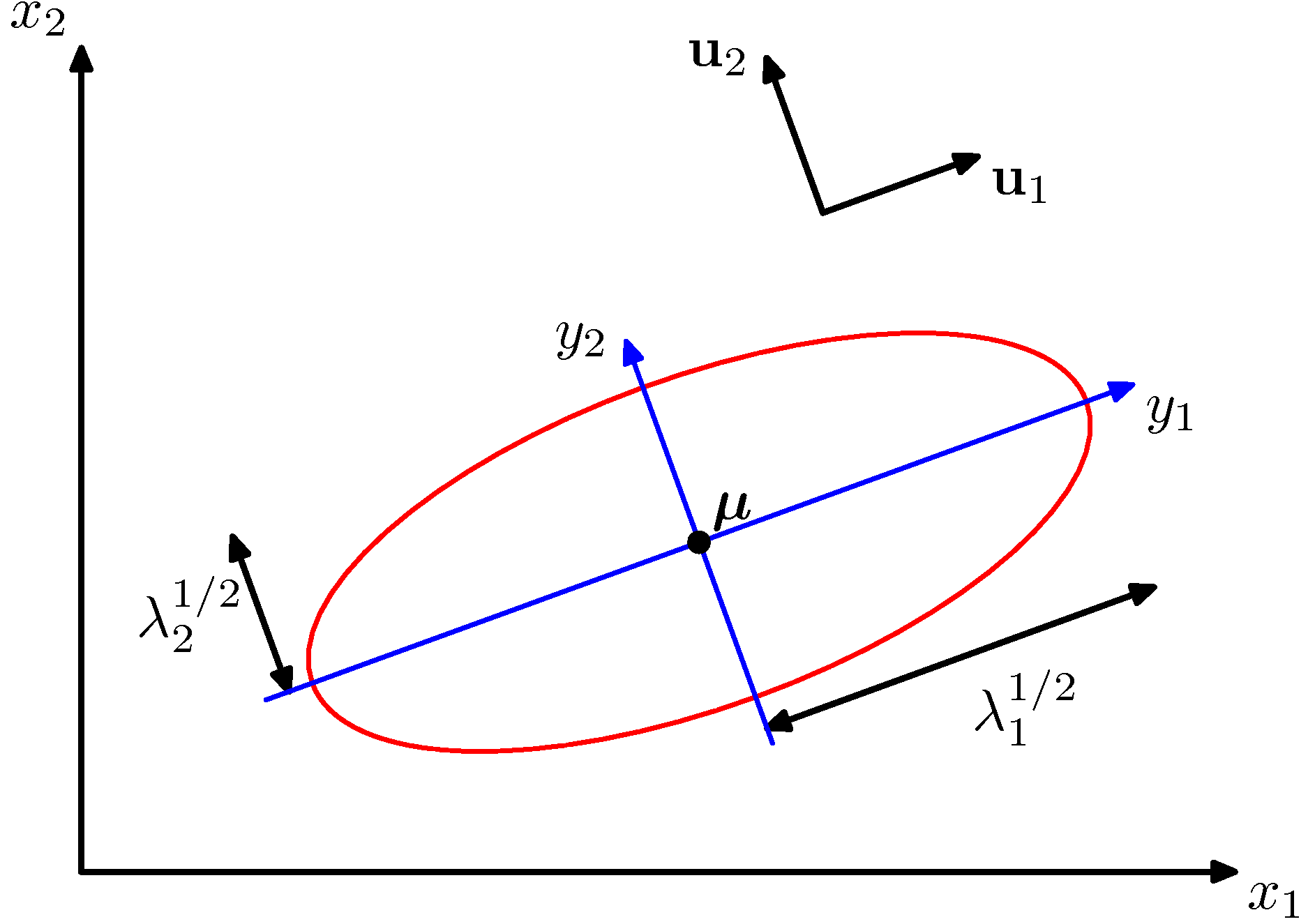Figure 2.7 이차원 공간 $\mathbf{x} = (x_1, x_2)$ 상에서의 상수 가우시안 확률 분포의 타원형 표면

만약 모든 고유값 $\lambda_i$들이 양의 값을 가진다면 이 표면은 타원형을 띱니다. 위 그림은 이를 보여줍니다. 타원형의 중심은 $\boldsymbol\mu$에 위치하며 타원형의 축은 $\mathbf{u}_i$에 자리합니다.

가우시안 분포를 더 잘 정의하기 위해서는 정규화를 위해 공분산 행렬의 모든 고윳값 $\lambda_i$들이 순양숫값을 가져야 합니다. 이런 행렬을 양의 정부호 positive definite 행렬이라고 합니다. 만약 0 또는 0보다 큰 값을 가질 경우에는 양의 준정부호 positive semidefinite 성질을 가졌다고 합니다.

이제 $y_i$로 정의되는 새로운 좌표 체계상에서의 가우시안 분포의 형태를 살펴보겠습니다. $\mathbf{x}$ 좌표계에서 $\mathbf{y}$ 좌표계로 변환되는 과정에서 야코비안 행렬 $\mathbf{J}$를 가집니다.

\[J_{ij} = \frac{\partial x_i}{\partial y_i} = U_{ji}\]

여기서 $U_{ji}$는 행렬 $\mathbf{U}^\text{T}$의 원소입니다. 행렬 $\mathbf{U}$의 정규직교성을 바탕으로 야코비안 행렬의 행렬식 제곱을 알 수 있습니다.

\[\vert\mathbf{J}\vert^2 = \vert\mathbf{U}^\text{T}\vert = \vert\mathbf{U}^\text{T}\vert\vert\mathbf{U}\vert=\vert\mathbf{U}^\text{T}\mathbf{U}\vert=\vert\mathbf{I}\vert=1\]

따라서 $\mathbf{J}=1$ 입니다. 또한 공분산 행렬의 행렬식 $\vert\boldsymbol{\Sigma}\vert$는 고윳값의 곱으로 표현할 수 있습니다.

\[\vert\boldsymbol{\Sigma}\vert^{1/2}=\prod^D_{j=1}\lambda^{1/2}_j\]

따라서 $y_j$ 좌표계에서 가우시안 분포는 다음의 형태를 가집니다.

\[p(\mathbf{y})=p(\mathbf{x})\vert\mathbf{J}\vert=\prod^D_{j=1}\frac{1}{(2\pi\lambda_j)^{1/2}}\exp\left\{-\frac{y_j^2}{2\lambda_j}\right\}\]

이는 $D$개의 독립적인 단변량 가우시안 분포들의 곱에 해당합니다. 따라서 고유 벡터들은 새로운 좌표축들을 표현하며 이때 결합 확률 분포는 이 좌표축에 따라 독립 분포들의 곱으로 인수분해됩니다.

\[\int p(\mathbf{y})d\mathbf{y} = \prod^D_{j=1}\int^\infty_{-\infty}\frac{1}{(2\pi\lambda_j)^{1/2}}\exp\left\{-\frac{y^2_j}{2\lambda_j}\right\}dy_j=1\]

위 식은 다변량 가우시안 분포가 정규화되었다는 것을 보여줍니다.

$\boldsymbol\mu$와 $\boldsymbol\Sigma$의 해석

이제 가우시안 분포의 모멘트값들을 살펴 매개변수 $\boldsymbol\mu$와 $\boldsymbol\Sigma$를 어떻게 해석할 수 있는지 알아보겠습니다.

$\boldsymbol\mu$

가우시안 분포에서의 $\mathbf{x}$의 기댓값은 다음과 같습니다.

\[\mathbb{E}[\mathbf{x}] = \frac{1}{(2\pi)^{D/2}}\frac{1}{\vert\boldsymbol\Sigma\vert^{1/2}}\int\exp\left\{-\frac12\mathbf{z}^\text{T}\boldsymbol\Sigma^{-1}\mathbf{z}\right\}(\mathbf{z}+\boldsymbol\mu)d\mathbf{z}\]

여기서 $\mathbf{z} = \mathbf{x} - \boldsymbol\mu$ 입니다. 이 식에서 지수 부분은 $\mathbf{z}$에 대해 짝함수 even function 임을 알 수 있습니다. 짝함수는 서로 덧셈 역원의 상이 서로 덧셈 역원인 함수를 의미합니다. $(\infty, -\infty)$ 범위에 대해 적분을 취하면 인자 $(\mathbf{z} + \boldsymbol\mu)$에 포함되어 있는 $\mathbf{z}$항이 대칭성에 의해 사라집니다. 따라서 다음과 같이 정리됩니다.

\[\mathbb{E}[\mathbf{x}] = \boldsymbol\mu\]

즉 $\boldsymbol\mu$값이 가우시안 분포의 평균값에 해당합니다.

$\boldsymbol\Sigma$

이제 가우시안 분포의 이차 모멘트 값을 살펴보겠습니다. 단변량 분포의 경우 이차 모멘트 값은 $\mathbb{E}[x^2]$입니다. 다변량 가우시안 분포의 경우 $\mathbb{E}[x_ix_j]$로 주어지는 이차 모멘트가 $D^2$만큼 존재합니다. 이들을 함께 묶어 행렬 $\mathbb{E}[\mathbf{x}\mathbf{x}^\text{T}]$로 만들 수 있습니다.

\[\mathbb{E}[\mathbf{x}\mathbf{x}^\text{T}] = \frac{1}{(2\pi)^{D/2}}\frac{1}{\vert\boldsymbol\Sigma\vert^{1/2}}\int\exp\left\{-\frac12\mathbf{z}^\text{T}\boldsymbol\Sigma^{-1}\mathbf{z}\right\}(\mathbf{z}+\boldsymbol\mu)(\mathbf{z}+\boldsymbol\mu)^\text{T}d\mathbf{z}\]

여기서도 $\boldsymbol\mu\mathbf{z}^\text{T}$와 $\mathbf{z}\boldsymbol\mu^{\text{T}}$ 등의 교차항들은 대칭성에 의해 사라집니다. $\boldsymbol\mu\boldsymbol\mu^\text{T}$는 상수이며 적분식 밖으로 빼낼 수 있습니다. 가우시안 분포가 정규화되어 있으므로 이 항의 값은 1입니다. $\mathbf{z}\mathbf{z}^\text{T}$을 포함한 항을 살펴보면, 고유 벡터를 이용해서 공분산 행렬을 전개하면 다음을 유도할 수 있습니다.

\[\mathbf{z} = \sum^D_{j=1}y_j\mathbf{u}_j\]

여기서 $y_j=\mathbf{u}_j^\text{T}\mathbf{z}$입니다. 이를 바탕으로 다음을 유도할 수 있습니다.

\[\frac{1}{(2\pi)^{D/2}}\frac{1}{\vert\boldsymbol\Sigma\vert^{1/2}}\int\exp\left\{-\frac12\mathbf{z}^\text{T}\boldsymbol\Sigma^{-1}\mathbf{z}\right\}\mathbf{z}\mathbf{z}^\text{T}d\mathbf{z} = \sum^D_{i=1}\mathbf{u}_i\mathbf{u}_i^\text{T}\lambda_i=\boldsymbol\Sigma\]

따라서 결과적으로 다음과 같습니다.

\[\mathbb{E}[\mathbf{x}\mathbf{x}^\text{T}]=\boldsymbol\mu\boldsymbol\mu^\text{T}+\boldsymbol\Sigma\]

이를 바탕으로 확률 벡터 $\mathbf{x}$의 공분산을 다음과 같이 정의할 수 있습니다.

\[\text{cov}[\mathbf{x}]=\mathbb{E}[(\mathbf{x}-\mathbb{E}[\mathbf{x}])(\mathbf{x}-\mathbb{E}[\mathbf{x}])^\text{T}]\]

가우시안 분포의 경우 $\mathbb{E}[\mathbf{x}]=\boldsymbol\mu$를 활용하여 다음을 구할 수 있습니다.

\[\text{cov}[\mathbf{x}]=\boldsymbol\Sigma\]

매개변수 행렬인 $\boldsymbol\Sigma$에 의해 가우시안 분산에서의 $\mathbf{x}$의 공분산이 결정됩니다. 그렇기 때문에 $\boldsymbol\Sigma$는 공분산 행렬이라고 불립니다.

가우시안 분포의 한계

가우시안 분포는 한 가지 치명적인 한계점을 가졌습니다. $\boldsymbol\Sigma$는 $D(D+1)/2$개의 독립적인 매개변수를 가집니다. 또한 $\boldsymbol\mu$에도 또 다른 $D$개의 독립적인 매개변수가 있습니다. 따라서 총 $D(D+3)/2$개의 매개변수를 가지게 됩니다. $D$값이 커질 경우 행렬을 다루고 역행렬을 계산하는 것이 매우 느려집니다.

이 문제를 해결하기 위해 제한된 형태의 공분산 행렬을 사용할 수 있습니다. 대각 행렬 diagonal matrix 의 형태를 지닌 공분산 행렬만을 사용한다면($\boldsymbol\Sigma = \text{diag}(\sigma^2))$ 총 $2D$개의 독립 매개변수만을 고려하면 됩니다.

공분산 행렬이 항등 행렬에 상수배만큼 비례하는 형태를 띠게($\boldsymbol\Sigma = \sigma^2\mathbf{I}$) 할 수도 있습니다. 이를 등방성 isotropic 공분산이라고 합니다. 이 경우 $D+1$개의 독립적인 매개변수를 가집니다.

이러한 방법을 활용해 자유도를 줄여 역행렬 계산을 훨씬 더 빠르게 할 수 있습니다. 하지만 확률 밀도의 형태를 상당히 제약시켜 모델의 성능이 떨어질 수 있습니다.

또 다른 한계점은 가우시안 분포가 단봉 unimodal 분포이기 때문에 다봉 multimodal 분포에 대해 적절한 근사치를 제공할 수 없다는 것입니다. 추후에 소개할 잠재 변수 latent variable을 이용해 이런 문제를 해결할 수 있습니다. 잠재 변수는 숨은 변수 hidden variable나 비관측 변수 unobserved variable라고 불립니다. 더 자세한 얘기는 나중에 다루겠습니다.

조건부 가우시안 분포

조건부 가우시안 분포

두 변수 집합이 결합적으로 가우시안 분포를 보인다면 하나의 변수 집합에 대한 다른 변수 집합의 조건부 분포 역시 가우시안 분포를 보입니다. 또한 각 변수 집합의 주변 분포 역시 가우시안 분포를 보입니다.

조건부 분포의 경우를 먼저 살펴보겠습니다. $D$차원의 벡터 $\mathbf{x}$가 $\mathcal{N}(\mathbf{x}\vert\boldsymbol\mu,\boldsymbol\Sigma)$의 가우시안 분포를 보인다고 가정하고 $\mathbf{x}$를 $\mathbf{x}_a, \mathbf{x}_b$로 나누겠습니다. $\mathbf{x}_a$가 $\mathbf{x}$의 첫 $M$ 원소에, $\mathbf{x}_b$가 나머지 $D - M$개의 원소에 해당한다고 가정할 수 있습니다. 그럼 다음과 같이 표현됩니다.

\[\begin{aligned} \mathbf{x} &= \binom{\mathbf{x}_a}{\mathbf{x}_b} \\ \boldsymbol\mu &= \binom{\boldsymbol\mu_a}{\boldsymbol\mu_b} \\ \boldsymbol\Sigma &= \begin{pmatrix}\boldsymbol\Sigma_{aa} \ \boldsymbol\Sigma_{ab} \\ \boldsymbol\Sigma_{ba} \ \boldsymbol\Sigma_{bb}\end{pmatrix} \\ \boldsymbol\Lambda&\equiv \boldsymbol\Sigma^{-1} \end{aligned}\]

여기서 $\boldsymbol\Lambda$를 정밀도 행렬이라고 부릅니다. 가우시안 분포의 몇몇 성질은 공분산으로 자연스럽게 표현할 수 있지만, 몇몇 성질들은 정밀도를 이용했을 때 더 쉽게 표현할 수 있습니다.

우선 조건부 분포 $p(\mathbf{x}_a\vert\mathbf{x}_b)$의 표현식을 찾아보겠습니다. 확률의 곱 법칙에 따라 이 조건부 분포를 결합 분포 $p(\mathbf{x}) = p(\mathbf{x}_a, \mathbf{x}_b)$로부터 계산할 수 있습니다. $\mathbf{x}_b$를 관측된 값으로 고정하고 그 결과에 해당하는 표현식을 정규화해서 $\mathbf{x}_a$에 해당하는 올바른 확률 분포를 구할 수 있습니다.

\[-\frac12(\mathbf{x}-\boldsymbol\mu)^{\text{T}}\boldsymbol\Sigma^{-1}(\mathbf{x}-\boldsymbol\mu) = \\ -\frac12(\mathbf{x}_a-\boldsymbol\mu_a)^{\text{T}}\boldsymbol\Lambda_{aa}(\mathbf{x}_a-\boldsymbol\mu_a) -\frac12(\mathbf{x}_a-\boldsymbol\mu_a)^{\text{T}}\boldsymbol\Lambda_{ab}(\mathbf{x}_b-\boldsymbol\mu_b) \\ -\frac12(\mathbf{x}_b-\boldsymbol\mu_b)^{\text{T}}\boldsymbol\Lambda_{ba}(\mathbf{x}_a-\boldsymbol\mu_a) -\frac12(\mathbf{x}_b-\boldsymbol\mu_b)^{\text{T}}\boldsymbol\Lambda_{bb}(\mathbf{x}_b-\boldsymbol\mu_b)\]

$\mathbf{x}_a$에 대해 결괏값은 이차식의 형태를 띠므로 이에 해당하는 조건부 분포 $p(\mathbf{x}_a\vert\mathbf{x}_b)$는 가우시안 분포입니다. 우리의 목표는 위 식을 활용하여 $p(\mathbf{x}_a\vert\mathbf{x}_b)$의 평균과 공분산을 찾는 것입니다. 이러한 과정을 제곱식의 완성 completing the square 이라고 합니다. 일반적인 가우시안 분포의 지수식 부분을 다음 식처럼 나타내어 제곱식의 완성 문제를 직접 풀어낼 수 있습니다.

\[-\frac12(\mathbf{x} - \boldsymbol\mu)^\text{T}\boldsymbol\Sigma^{-1}(\mathbf{x} - \boldsymbol\mu) = -\frac12\mathbf{x}^\text{T}\boldsymbol\Sigma^{-1}\mathbf{x}+\mathbf{x}^\text{T}\boldsymbol\Sigma^{-1}\boldsymbol\mu + \text{const}\]

여기서 $\text{const}$는 $\mathbf{x}$에 대해 독립적인 항들입니다. 또한 $\boldsymbol\Sigma$가 대칭이라는 점을 이용했습니다. 우리가 풀고자 하는 일반 형태의 이차식을 위 식의 오른쪽 변의 형태로 표현하면 $\mathbf{x}$의 이차항에 해당하는 계수들의 행렬과 공분산 행렬의 역행렬 $\boldsymbol\Sigma^{-1}$이 같고 $\mathbf{x}$의 일차항의 계수들과 $\boldsymbol\Sigma^{-1}\boldsymbol\mu$가 같다는 것을 알 수 있습니다. 이를 바탕으로 $\boldsymbol\mu$를 계산할 수 있습니다.

이 과정을 조건부 가우시안 분포 $p(\mathbf{x}_a\vert\mathbf{x}_b)$에 적용해보겠습니다. $\mathbf{x}_a$의 이차식에 해당하는 항만 골라내면 다음과 같습니다.

\[-\frac12\mathbf{x}_a^\text{T}\boldsymbol\Lambda_{aa}\mathbf{x}_a\]

이를 바탕으로 $p(\mathbf{x}_a\vert\mathbf{x}_b)$의 공분산을 다음과 같이 구할 수 있습니다.

\[\boldsymbol\Sigma_{a\vert b}=\boldsymbol\Lambda_{aa}^{-1}\]

이번에는 $\mathbf{x}_a$의 일차식에 해당하는 항만 추려내겠습니다.

\[\mathbf{x}_a^\text{T}\{\boldsymbol\Lambda_{aa}\boldsymbol\mu_a-\boldsymbol\Lambda_{ab}(\mathbf{x}_b-\boldsymbol\mu_b)\}\]

여기서 다음을 구할 수 있습니다.

\[\boldsymbol\mu_{a\vert b} = \boldsymbol\mu_a - \boldsymbol\Lambda_{aa}^{-1}\boldsymbol\Lambda_{ab}(\mathbf{x}_b-\boldsymbol\mu_b)\]

이렇게 분할 정밀 행렬에 대한 식을 통해 결괏값을 구했습니다. 이 평균과 공분산은 공분산 행렬 $\boldsymbol\Sigma$의 식으로도 표현이 가능합니다. 결과만 살펴보면 다음과 같습니다.

\[\begin{aligned} \boldsymbol\mu_{a\vert b} &= \boldsymbol\mu_a + \boldsymbol\Sigma_{ab}\boldsymbol\Sigma_{bb}^{-1}(\mathbf{x}_b-\boldsymbol\mu_b)\\ \boldsymbol\Sigma_{a\vert b} &= \boldsymbol\Sigma_{aa} - \boldsymbol\Sigma_{ab}\boldsymbol\Sigma^{-1}_{bb}\boldsymbol\Sigma_{ba} \end{aligned}\]

위 식을 살펴보면 조건부 분포 $p(\mathbf{x}_a\vert\mathbf{x}_b)$를 표현할 때는 분할 정밀 행렬을 사용하는 것이 더 단순한 형태를 띤다는 것을 알 수 있습니다. 위 식의 $p(\mathbf{x}_a\vert\mathbf{x}_b)$의 평균은 $\mathbf{x}_b$에 대한 일차식이며 공분산은 $\mathbf{x}_b$에 대해 독립적입니다. 이것이 바로 선형 가우시안 linear Gaussian의 예시입니다.

주변 가우시안 분포

결합 분포 $p(\mathbf{x}_a, \mathbf{x}_b)$가 가우시안 분포이면 $p(\mathbf{x}_a\vert\mathbf{x}_b)$도 가우시안 분포임을 확인하였습니다. 이제는 다음의 식으로 주어지는 주변 분포에 대해 살펴보겠습니다.

\[p(\mathbf{x}_a) = \int p(\mathbf{x}_a, \mathbf{x}_b)d\mathbf{x}_b\]

위 식 역시 가우시안 분포입니다. 결과는 다음과 같습니다.

\[\begin{aligned} \mathbb{E}[\mathbf{x}_a] &= \boldsymbol\mu_a \\ \text{cov}[\mathbf{x}_a] &= \boldsymbol\Sigma_{aa}\end{aligned}\]

이 결과는 우리의 직관과도 일치합니다. 조건부 분포와는 달리 주변 분포의 경우 분할 공분산 행렬을 활용할 때 평균과 공분산이 더 단순하게 표현됩니다.

요약

많은 식이 나왔으므로 분할 가우시안 분포의 조건부 분포와 주변 분포에 대해 요약해보겠습니다.

결합 가우시안 분포 $\mathcal{N}(\mathbf{x}\vert\boldsymbol\mu, \boldsymbol\Sigma)$가 주어졌으며 $\boldsymbol\Lambda \equiv \boldsymbol\Sigma^{-1}$인 경우

조건부 분포는 다음과 같습니다.

\[\begin{aligned} p(\mathbf{x}_a\vert\mathbf{x}_b) &= \mathcal{N}(\mathbf{x}_a\vert\boldsymbol\mu_{a\vert b}, \boldsymbol\Lambda_{aa}^{-1}) \\ \boldsymbol\mu_{a\vert b} &= \boldsymbol\mu_a - \boldsymbol\Lambda_{aa}^{-1}\boldsymbol\Lambda_{ab}(\mathbf{x}_b-\boldsymbol\mu_b) \end{aligned}\]

주변 분포는 다음과 같습니다.

\[p(\mathbf{x}_a) = \mathcal{N}(\mathbf{x}_a\vert\boldsymbol\mu_{a},\boldsymbol\Sigma_{aa})\]

가우시안 분포의 총합

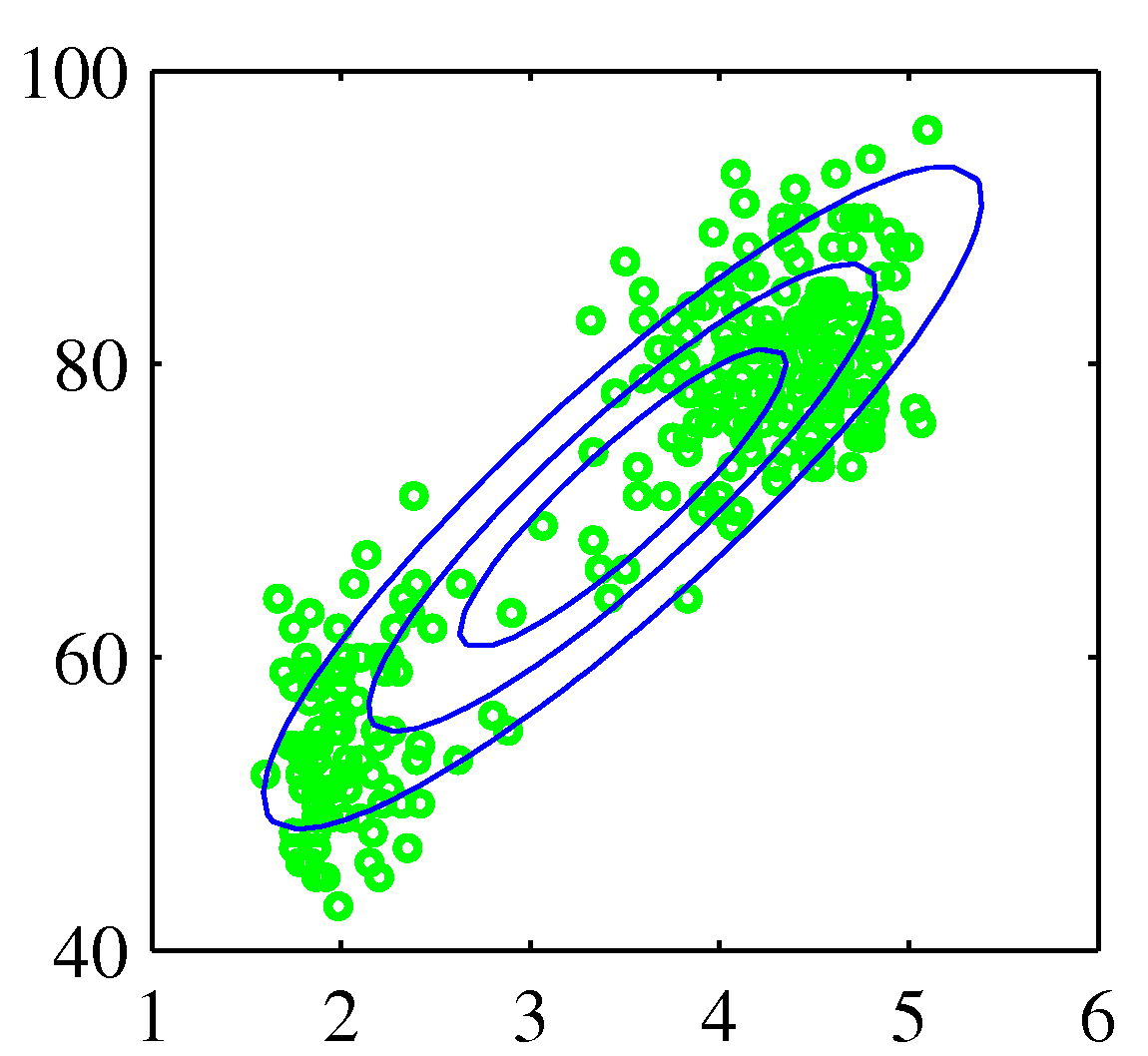
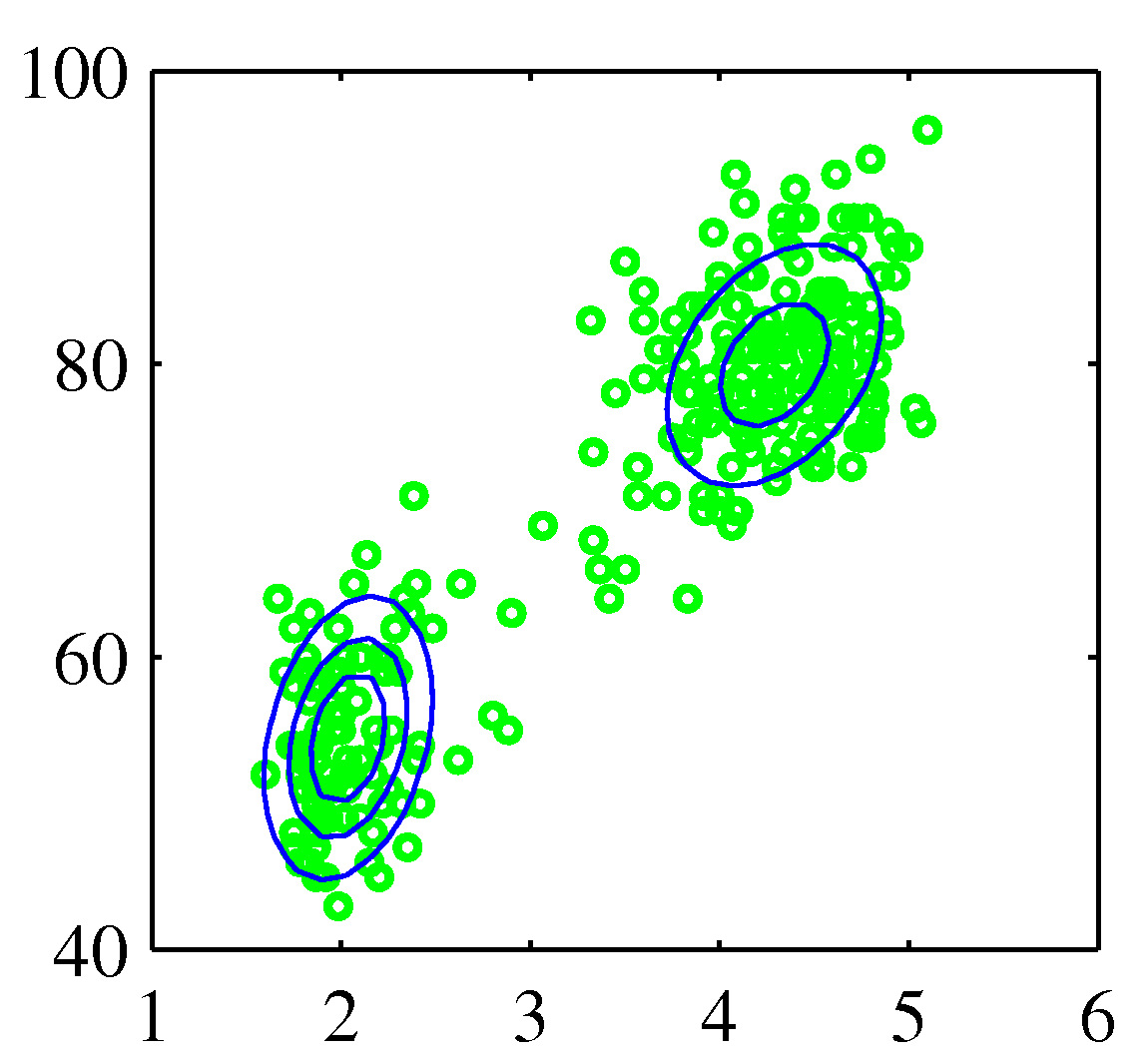
Figure 2.21 간헐 온천의 분화에 대한 분포

가우시안 분포는 실제 데이터 집합을 모델링하는 데는 한계점을 가지고 있습니다. 위 사례처럼 데이터가 두 개의 무리로 나누어져 있을 경우 하나의 가우시안 분포로는 이 구조를 잘 표현하지 못 합니다. 하지만 두 가우시안 분포를 선형 중첩하면 이 데이터 집합을 표현할 수 있습니다. 이런 확률 모델들을 혼합 분포 mixture distribution 이라고 합니다. 충분히 많은 숫자의 가우시안 분포를 사용한다면 거의 모든 연속 밀도를 임의의 정확도로 근사할 수 있습니다.

\[p(\mathbf{x})=\sum^K_{k=1}\pi_k\mathcal{N}(\mathbf{x}\vert\boldsymbol\mu_k,\boldsymbol\Sigma_k)\]

위 식은 K개의 가우시안 밀도 중첩으로, 가우시안 혼합 분포 mixture of Gaussians 라고 부릅니다. 각각의 가우시안 밀도 함수는 혼합의 성분 component이며 각 성분은 각각 평균과 공분산을 가지고 있습니다. 매개변수 $\pi_k$는 혼합 계수 mixing coefficient 입니다. 위 식의 양변을 $\mathbf{x}$에 대해 적분하고 $p(\mathbf{x})$와 개별 가우시안 성분들이 정규화되어 있다는 점을 고려하면 다음과 같습니다.

\[\sum^K_{k=1}\pi_k=1\]

또한 가우시안 밀도 함수가 0 이상의 값을 가진다는 전제 조건하에 모든 $k$에 대해 $\pi_k \geq 0$이라는 것이 $p(\mathbf{x}) \geq 0$이라는 조건을 만족시키기 위한 충분 조건이 됩니다. 이를 고려하면 $0 \leq \pi_k \leq 1$ 임을 알 수 있습니다. 이로부터 혼합 계수들이 확률의 조건을 만족시킨다는 것을 알 수 있습니다. 확률의 합과 곱의 법칙을 활용하여 주변 밀도가 다음과 같음을 알 수 있습니다.

\[p(\mathbf{x}) = \sum^K_{k=1}p(k)p(\mathbf{x}\vert k)\]

앞서 보았던 가우시안 혼합 분포 식에서 $\pi_k = p(k)$는 $k$번째 성분을 뽑을 사전 확률로 볼 수도 있고 밀도 $\mathcal{N}(\mathbf{x}\vert\boldsymbol\mu_k, \boldsymbol\Sigma_k) = p(\mathbf{x}\vert k)$는 $k$가 주어졌을 때의 $\mathbf{x}$의 확률로 볼 수 있습니다. 결과적으로 위 식과 가우시안 혼합 분포식은 같습니다. 여기서 사후 확률 $p(k\vert\mathbf{x})$를 책임값 responsibilities라고 합니다. 이 값에 대해서는 앞으로 계속해서 더 자세히 다룰 것입니다. 베이지안 정리에 따라서 이 사후 확률은 다음과 같습니다.

\[\begin{aligned} \gamma_k(\mathbf{x}) &\equiv p(k\vert\mathbf{x}) \\ &= \frac{p(k)p(\mathbf{x}\vert k)}{\sum_lp(l)p(\mathbf{x}\vert l)} \\ &= \frac{\pi_k\mathcal{N}(\mathbf{x}\vert\boldsymbol\mu_k,\boldsymbol\Sigma_k)}{\sum_l\pi_l\mathcal{N}(\mathbf{x}\vert\boldsymbol\mu_l,\boldsymbol\Sigma_l)} \end{aligned}\]

가우시안 혼합 분포의 형태는 매개변수 $\boldsymbol\pi, \boldsymbol\mu, \boldsymbol\Sigma$로 결정됩니다. 이 매개변수들의 값을 찾기 위해서는 최대 가능도 방법을 사용할 수 있습니다. 가우시안 혼합 분포의 식으로부터 로그 가능도 함수는 다음과 같이 주어집니다.

\[\ln p(\mathbf{X}\vert\boldsymbol\pi, \boldsymbol\mu, \boldsymbol\Sigma)=\sum^N_{n=1}\ln\left\{\sum^K_{k=1}\pi_k\mathcal{N}(\mathbf{x}_n\vert\boldsymbol\mu_k,\boldsymbol\Sigma_k)\right\}\]

여기서 $\mathbf{X} = {\mathbf{x}_1, …, \mathbf{x}_N}$ 입니다. 로그 안에 $k$에 대한 합산이 포함되어 있어 단일 가우시안 분포에 비해 더 복잡합니다. 이 함수의 최댓값을 구하기 위해서는 반복적인 수치적 최적화 테크닉이나 기댓값 최대화 expectation maximization 등의 방법을 사용할 수 있습니다. 이 방법에 대해서는 나중에 다루겠습니다.

working in progress..