[PRML] Chapter 3. Linear Regression (1) - 선형 기저 함수 모델
본 글은 책 ‘패턴 인식과 머신 러닝’의 국내 출판본을 바탕으로 작성되었습니다.
3.0 도입
지금까지는 비지도 학습에 대해 살펴봤다면 이제 지도 학습에 대해 살펴보겠습니다. 회귀 모델의 목표는 $D$차원의 벡터 $\mathbf{x}$들이 입력 input 변수로 주어졌을 때, 그에 해당하는 연속하는 타깃 target 변수 $t$ 값을 예측하는 것입니다. 가장 단순한 형태의 선형 회귀 모델은 입력 변수들에 대한 선형 함수이지만, 입력 변수들에 대한 비선형 함수들의 집합을 선형적으로 결합할 수도 있습니다. 이러한 함수들을 기저 함수 basis function 이라고 합니다.
가장 단순한 접근은 새 입력값 $\mathbf{x}$에 대해 해당 표적값 $t$를 출력하도록 하는 적절한 함수 $y(\mathbf{x})$를 만드는 것입니다. 확률적인 측면에서는 예측 분포 $p(t\vert\mathbf{x}$)를 모델하는 것이라고 할 수 있습니다. 이 조건부 분포를 이용하면 어떤 새 $\mathbf{x}$에 대해서든 손실 함수의 기댓값을 최소화하는 표적값 $t$를 예측해낼 수 있습니다.
3.1 선형 기저 함수 모델
가장 단순한 형태의 선형 회귀 모델은 입력 변수들의 선형 결합을 바탕으로 한 모델입니다.
\[y(\mathbf{x}, \mathbf{w}) = w_0 + w_1x_1 + ... + w_Dx_D\]여기서 $\mathbf{x} = (x_1, …, x_D)^\text{T}$ 입니다. 이 모델은 선형 회귀 linear regression 라고도 불립니다. 이 모델의 가장 중요한 성질은 매개변수 $w_0, …, w_D$의 선형 함수라는 것입니다. 또한 입력 변수 $x_i$의 선형 함수이기도 한데 이 성질이 선형 회귀 모델의 한계점이 됩니다. 이를 극복하기 위해 고정 비선형 함수들의 선형 결합을 사용할 수 있습니다.
\[y(\mathbf{x}, \mathbf{w}) = w_0 + \sum^{M-1}_{j=1}w_j\phi_j(\mathbf{x})\]여기서 $\phi_j(\mathbf{x})$가 기저 함수 basis function 입니다. 매개변수 $w_0$은 편향 bias라고도 부르며, 데이터의 고정된 치우침을 표현하도록 도와줍니다.
\[y(\mathbf{x},\mathbf{w}) = \sum^{M-1}_{j=0}w_j\phi_j(\mathbf{x})=\mathbf{w}^\text{T}\boldsymbol{\phi}(\mathbf{x})\]$\phi_0(\mathbf{x}) = 1$이라고 가정하면 위와 같이 표현할 수 있습니다. $\mathbf{w} = (w_0, …, w_{M-1})^\text{T}$이고 $\boldsymbol{\phi} = (\phi_0, …, \phi_{M-1})^\text{T}$ 입니다. 원 데이터 변수에 전처리나 특징 추출 과정을 적용하게 되는데 이러한 특징들을 기저 함수 $\phi_j(\mathbf{x})$를 바탕으로 표현할 수 있습니다.
다항 기저 함수의 한 가지 한계점은 이 함수가 입력 변수에 대한 전역적인 함수이기 때문에 입력 공간의 한 영역에서 발생한 변화가 다른 영역에까지 영향을 미친다는 것입니다. 이를 해결하기 위해 입력 공간을 여러 영역들로 나누고 각 영역에 대해 서로 다른 다항식을 피팅할 수 있습니다. 이를 스플라인 함수 spline function 이라고 합니다.
다양한 다른 함수들이 기저 함수로 사용될 수 있습니다.
\[\phi_j(x) = \exp\left\{-\frac{(x-\mu_j)^2}{2s^2}\right\}\]여기서 $\mu_j$는 입력 공간에서의 기저 함수의 위치를 결정하며 매개변수 $s$는 공간적 크기를 결정합니다. 위 식은 보통 가우시안 기저 함수라고 불립니다. 적응 매개변수 $w_j$가 곱해지므로 정규화 계수는 중요하지 않습니다.
\[\phi_j(x)=\sigma\left(\frac{x-\mu_j}{s}\right)\]위 식은 또 다른 기저 함수의 예입니다. 시그모이드 기저 함수입니다. 여기서 $\sigma(a) = \frac{1}{1+\exp(-a)}$ 입니다. tanh 함수와 로지스틱 시그모이드 함수는 $\tanh(a) = 2\sigma(2a)-1$이라는 관계를 가졌으므로 로지스틱 시그모이드 함수의 선형 결합은 결국 tanh 함수의 선형 결합으로 표현됩니다.
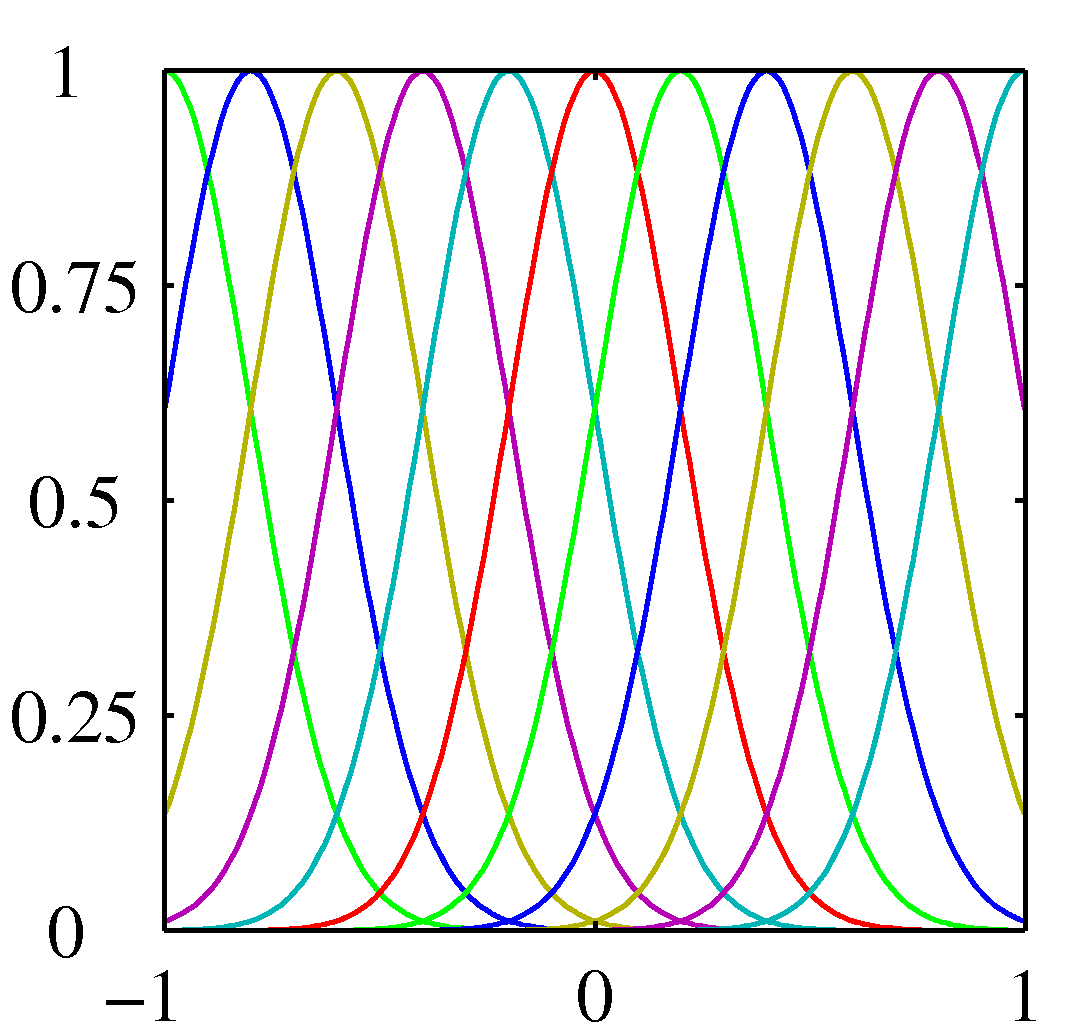
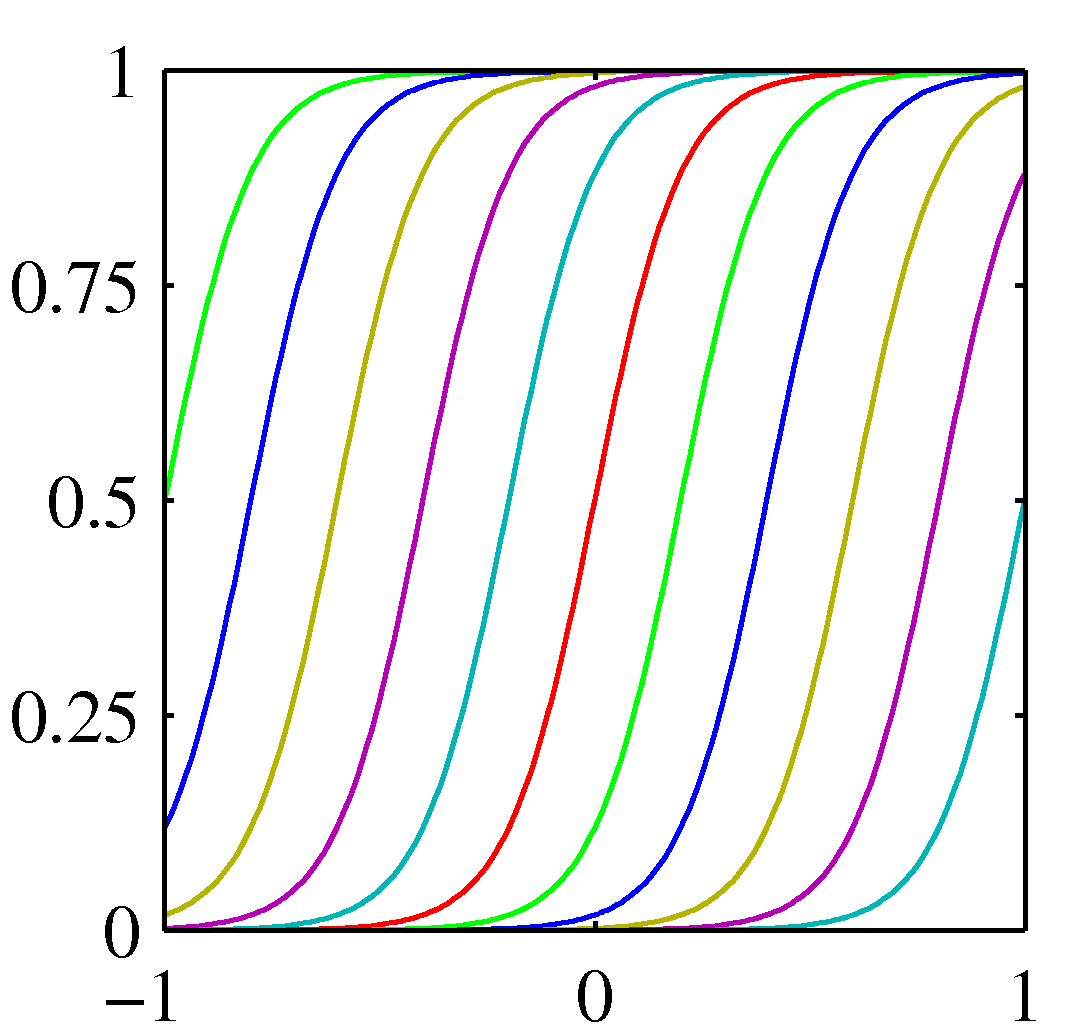
Figure 3.1 기저 함수의 예시들. 각각 다항 기저 함수, 가우시간 기저 함수, 시그모이드 기저 함수
앞으로 다룰 내용들은 어떤 기저 함수를 사용하는지와 무관합니다. 기저 함수가 단순히 항등 함수 $\boldsymbol{\phi}(\mathbf{x}) = \mathbf{x}$일 때도 적용 가능합니다.
최대 가능도와 최소 제곱
1장에서 제곱합 오류 함수를 최소화하는 방식으로 데이터 집합에 다항 함수를 근사했으며 이 오류 함수를 최소화하는 것이 최대 가능도 해를 구하는 것과 같다는 것을 증명했습니다. 이 관계에 더해 더 자세히 살펴보도록 하겠습니다.
\[t = y(\mathbf{x}, \mathbf{w}) + \epsilon\]여기서 $\epsilon$는 0을 평균으로, $\beta$를 정밀도로 가지는 가우시안 노이즈를 의미합니다. 따라서 다음과 같습니다.
\[p(t\vert\mathbf{x}, \mathbf{w}, \beta) = \mathcal{N}(t\vert y(\mathbf{x},\mathbf{w}),\beta^{-1})\]제곱 오류 함수를 가정할 경우 새 변수 $\mathbf{x}$에 대한 최적의 예측값은 타깃 변수의 조건부 평균으로 주어집니다. 위 식의 형태의 가우시안 조건부 분포의 경우 조건부 평균은 다음과 같습니다.
\[\mathbb{E}[t\vert\mathbf{x}]=\int tp(t\vert\mathbf{x})dt = y(\mathbf{x}, \mathbf{w})\]노이즈의 분포가 가우시안이라는 가정은 $\mathbf{x}$가 주어졌을 때의 $t$의 조건부 분포가 단봉 형태임을 의미합니다.
입력 데이터 집합 $\mathbf{X} = {\mathbf{x}_1, …, \mathbf{x}_N}$과 그에 해당하는 타깃 변수 $t_1, …, t_N$을 고려해보겠습니다. 타깃 변수들 ${t_n}$을 $\mathbf{t}$로 지칭한 열 벡터로 무리지을 수 있습니다. 이 데이터들이 위 식의 분포로부터 독립적으로 추출되었다고 가정한다면 다음과 같은 가능도 함수를 얻을 수 있습니다.
\[p(\mathbf{t}\vert\mathbf{X},\mathbf{w},\beta) = \prod^N_{n=1}\mathcal{N}(t_n\vert\mathbf{w}^\text{T}\boldsymbol\phi(\mathbf{x}_n),\beta^{-1})\]지도 학습 문제의 경우 우리는 입력 변수의 분포를 모델링 하지는 않으므로 $\mathbf{x}$는 언제나 조건부 변수의 집합에 포함되어 있습니다. 따라서 표현식에서도 $\mathbf{x}$를 뺄 수 있습니다. 가능도 함수에 대해 로그를 취하고 단변량 가우시안의 표준 형태 식을 이용하면 다음을 얻습니다.
\[\begin{aligned} \ln p(\mathbf{t}\vert\mathbf{w},\beta) &= \sum^N_{n=1}\ln\mathcal{N}(t_n\vert\mathbf{w}^\text{T}\boldsymbol\phi(\mathbf{x}_n),\beta^{-1}) \\ &= \frac N2\ln\beta-\frac N2\ln(2\pi)-\beta E_D(\mathbf{w}) \end{aligned}\]여기서 제곱합 오류 함수는 다음과 같습니다.
\[E_D(\mathbf{w})=\frac12\sum^N_{n=1}\{t_n-\mathbf{w}^\text{T}\boldsymbol\phi(\mathbf{x}_n)\}^2\]가능도 함수를 구했으므로 최대 가능도 방법을 적용하여 $\mathbf{w}$와 $\beta$를 구할 수 있습니다. 첫 번째로 $\mathbf{w}$에 대해 극대화하는 경우를 고려해보겠습니다. 위 식의 로그 가능도 함수의 기울기는 다음과 같습니다.
\[\nabla\ln p(\mathbf{t}\vert\mathbf{w},\beta) = \beta\sum^N_{n=1}\{t_n-\mathbf{w}^\text{T}\boldsymbol\phi(\mathbf{x}_n)\}\boldsymbol\phi(\mathbf{x}_n)^\text{T}\]기울기를 0으로 놓으면 다음을 얻게 됩니다.
\[0 = \sum^N_{n=1}t_n\boldsymbol\phi(\mathbf{x}_n)^\text{T}-\mathbf{w}^\text{T}\left(\sum^N_{n=1}\boldsymbol{\phi}(\mathbf{x}_n)\boldsymbol{\phi}(\mathbf{x}_n)^\text{T}\right)\]이를 $\mathbf{w}$에 대해 풀면 다음과 같습니다.
\[\mathbf{w}_\text{ML} = (\mathbf{\Phi}^\text{T}\mathbf\Phi)^{-1}\mathbf\Phi^\text{T}\mathbf{t}\]
위 식을 최소 제곱 문제의 정규 방정식 normal equation 이라고 합니다. 여기서 $\mathbf\Phi$는 $N \times M$ 행렬로, 설계 행렬 design matrix 라고 부릅니다. 설계 행렬의 각 원소는 $\Phi_{nj}=\phi_j(\mathbf{x}_n)$으로 주어집니다.
\[\mathbf\Phi = \begin{pmatrix} \phi_0(\mathbf{x_1}) & \phi_1(\mathbf{x_1}) & \cdots & \phi_{M-1}(\mathbf{x_1}) \\ \phi_0(\mathbf{x_2}) & \phi_1(\mathbf{x_2}) & \cdots & \phi_{M-1}(\mathbf{x_2}) \\ \vdots & \vdots & \ddots & \vdots \\ \phi_0(\mathbf{x_N}) & \phi_1(\mathbf{x_N}) & \cdots & \phi_{M-1}(\mathbf{x_N}) \end{pmatrix}\] \[\mathbf\Phi^\dagger \equiv (\mathbf\Phi^\text{T}\mathbf\Phi)^{-1}\mathbf\Phi^\text{T}\]위 식을 행렬 $\mathbf\Phi$의 무어-펜로즈 유사-역 Moor-Penrose pseudo-inverse라고 합니다. 역행렬의 개념을 정사각이 아닌 행렬들에 대해서 일반화한 것입니다.
이제 편향 매개변수 $w_0$의 역할에 대해 살펴보겠습니다. 편향 매개변수를 명시화하면 오류 함수를 다음과 같이 적을 수 있습니다.
\[E_D(\mathbf{w})=\frac12\sum^N_{n=1}\{t_n-w_0-\sum^{M-1}_{j=1}w_j\phi_j(\mathbf{x}_n)\}^2\]$w_0$에 대한 미분값을 0으로 놓고 $w_0$에 대해 풀면 다음과 같습니다.
\[w_0 = \overline{t}-\sum^{M-1}_{j=1}w_j\overline{\phi_j}\]여기서 $\overline{t} = \frac1N\sum^N_{n=1}t_n$ 이며 $\overline{\phi_j} = \frac1N\sum^N_{n=1}\phi_j(\mathbf{x}_n)$ 입니다. 편향 $w_0$가 훈련 집합의 타깃 변수들의 평균과 기저 함숫값 평균들의 가중 합 사이의 차이를 보상하고 있음을 알 수 있습니다.
또한 로그 가능도 함수를 노이즈 정밀도 매개변수 $\beta$에 대해 최대화하면 다음과 같습니다.
\[\frac1{\beta_\text{ML}} = \frac1N\sum^N_{n=1}\{t_n-\mathbf{w}^\text{T}_\text{ML}\boldsymbol\phi(\mathbf{x}_n)\}^2\]노이즈 정밀도의 역이 회귀 함수 근처 타깃 변수들의 잔차 분산으로 주어진다는 것을 알 수 있습니다.
최소 제곱의 기하학적 의미
최소 제곱 해의 기하학적 의미를 살펴보겠습니다. $N$차원의 공간을 가정해 보겠습니다. 이 공간의 축들은 $t_n$으로 주어지며 $\mathbf{t} = (t_1, …, t_N)^\text{T}$는 이 공간상의 벡터에 해당합니다. 각각의 기저 함수 $\phi_j(\mathbf{x}_n)$들을 $N$개의 데이터들에 대해 계산한 값 역시 공간 상의 벡터 $\varphi_j$로 표현 가능합니다. 그림으로 표현하면 다음과 같습니다.
Figure 3.2 $t_1, …, t_N$을 축으로 가지는 $N$차원 공간상에서의 최소 제곱 해의 기하학적 의미
$\mathbf{y}$를 $n$번째 원소가 $y(\mathbf{x}_n, \mathbf{w})$로 주어지는 $N$차원의 벡터라고 정의한다면 제곱합 오류는 $\mathbf{y}$와 $\mathbf{t}$ 간의 제곱 유클리드 거리에 해당합니다.
순차적 학습
앞서 살펴본 최대 가능도 해와 같은 일괄 처리 테크닉을 활용하기 위해서는 전체 훈련 집합을 한 번에 처리해야 합니다. 큰 데이터 집합에 대해서는 이러한 방식이 계산적으로 복잡할 수 있습니다. 따라서 이러한 경우 순차적 sequential 알고리즘 (온라인 on-line 알고리즘)을 활용할 수 있습니다. 한번에 하나의 데이터를 고려하며 모델의 매개변수들은 그때마다 업데이트됩니다.
이를 위해 확률적 경사 하강법 stochastic gradient descent / 순차적 경사 하강법 sequential gradient descent를 적용할 수 있습니다. 만약 여러 데이터들에 대한 오류 함수의 값이 데이터 포인트 각각의 오류 함수의 값을 합한 것과 같다면 확률적 경사 하강법을 이용해서 패턴 $n$이 등장한 후의 매개변수 벡터 $\mathbf{w}$를 다음과 같이 업데이트 할 수 있습니다.
\[\mathbf{w}^{(\tau+1)}=\mathbf{w}^{(\tau)}-\eta\nabla E_n\]여기서 $\tau$는 반복수를 의미하며 $\eta$는 학습률을 의미합니다. 시작 시에는 $\mathbf{w}$의 값을 어떤 시작 벡터 $\mathbf{w}^{(0)}$으로 초기화합니다. 제곱합 오류 함수의 경우 식은 다음과 같습니다.
\[\mathbf{w}^{(\tau+1)} = \mathbf{w}^{(\tau)}+\eta(t_n-\mathbf{w}^{(\tau)\text{T}}\boldsymbol\phi_n)\boldsymbol\phi_n\]
이를 최소 제곱 평균 least mean square, LMS 알고리즘이라고 합니다.
정규화된 최소 제곱법
앞서 1장에서 과적합 문제를 막기 위해서 오류 함수에 정규화항을 추가하는 아이디어에 대해 소개했습니다. 이를 포함한 오류 함수는 다음의 형태를 가집니다.
\[E_D(\mathbf{w}) + \lambda E_W(\mathbf{w})\]여기서 $\lambda$는 데이터에 종속적인 에러 $E_D(\mathbf{w})$와 정규화항 $E_W(\mathbf{w}$의 상대적인 중요도를 조절하기 위한 정규화 상수입니다. 가장 단순한 형태의 정규화항은 가중치 벡터 원소들의 제곱합입니다.
\[E_W(\mathbf{w})=\frac12\mathbf{w}^\text{T}\mathbf{w}\]다음의 형태로 주어지는 제곱합 오류 함수를 고려해보겠습니다.
\[E_D(\mathbf{w})=\frac12\sum^N_{n=1}\{t_n-\mathbf{w}^\text{T}\boldsymbol\phi(\mathbf{x}_n)\}^2\]위 두 식을 함께 고려하면 전체 오류 함수는 다음과 같습니다.
\[\frac12\sum^N_{n=1}\{t_n-\mathbf{w}^\text{T}\boldsymbol\phi(\mathbf{x}_n)\}^2+\frac\lambda2\mathbf{w}^\text{T}\mathbf{w}\]해당 형태의 정규화항은 가중치 감쇠 weight decay라고 부릅니다. 순차 학습 알고리즘에서 해당 정규화항을 사용할 경우 데이터에 지지되지 않는 한 가중치의 값이 0을 향해 감소합니다. 통계학에서 이는 매개변수값이 0을 향해 축소되므로 매개변수 축소 parameter shrinkage 방법의 예시입니다. 이 정규화항을 쓰면 오류 함수가 $\mathbf{w}$의 이차 함수의 형태로 유지되며 따라서 오류 함수를 최소화하는 값을 닫힌 형태로 찾아낼 수 있습니다. 위 식의 $\mathbf{w}$에 대한 기울기를 0으로 놓고 풀어내면 다음과 같습니다.
\[\mathbf{w} = (\lambda\mathbf{I} + \mathbf{\Phi}^\text{T}\mathbf{\Phi})^{-1}\mathbf{\Phi}^\text{T}\mathbf{t}\]좀 더 일반적인 형태의 정규화항을 사용할 수도 있습니다. 이 경우 정규화 오류 함수는 다음과 같습니다.
\[\frac12\sum^N_{n=1}\{t_n-\mathbf{w}^\text{T}\boldsymbol\phi(\mathbf{x}_n)\}^2+\frac\lambda2\sum^M_{j=1}\vert w_j\vert^q\]$q=2$인 경우 이는 앞서 보았던 이차 정규화항에 해당합니다.
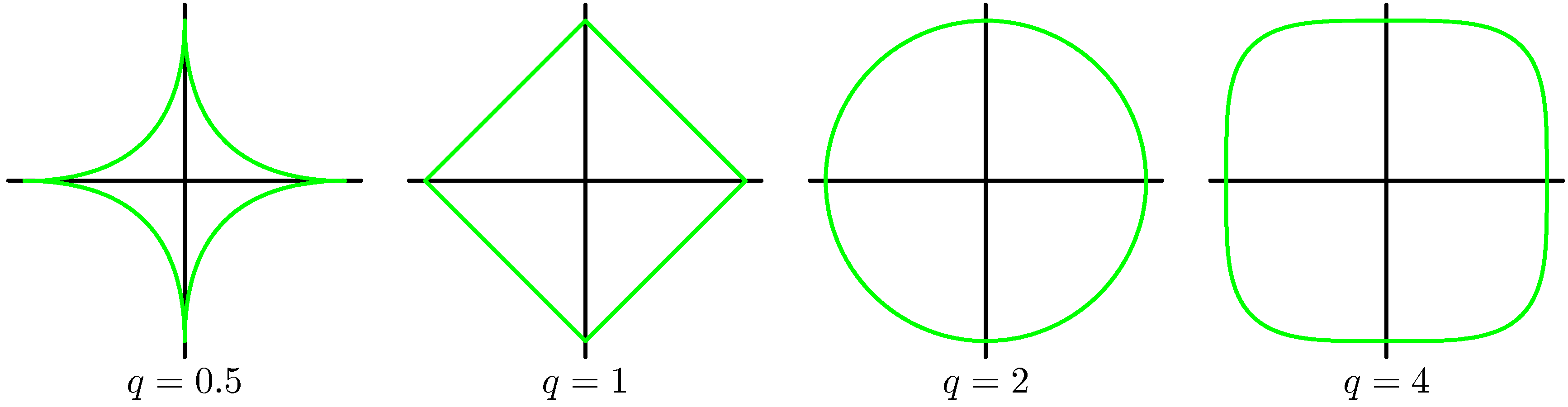Figure 3.3 다양한 매개변수 $q$값에 따른 정규화항의 윤곽선
위 그림에서 매개변수 $q$값에 따른 정규화 함수의 윤곽선을 확인할 수 있습니다. $q = 1$일 경우를 일컬어 라쏘 lasso라고 합니다. 라쏘 정규화를 시행할 경우 $\lambda$의 값을 충분히 크게 설정하면 몇몇 계수 $w_j$가 0이 되며 이런 모델을 희박한 sparse 모델이라고 합니다. 계수가 0이 된 해당 항의 기저 함수는 더 이상 사용되지 않습니다.
정규화는 모델의 복잡도를 제한하여 복잡한 모델들이 제한된 수의 데이터 집합을 이용해서도 심각한 과적합 없이 피팅될 수 있습니다. 이를 위해서는 적절한 정규화 계수 $\lambda$를 찾아야합니다.
다중 출력값
지금까지 단일 타깃 변수 $t$에 대해서만 고려했습니다. 몇몇 응용 사례의 경우 여러 개의 타깃 변수에 대해서 예측하는 것이 필요할 수 있습니다. $\mathbf{t}$의 각 성분들에 대해서 다른 기저 함수 집합을 사용해서 이를 달성할 수 있지만, 같은 종류의 기저 함수를 표적 벡터의 각 성분들에 동일하게 사용하여 모델하는 방법이 더 널리 사용됩니다.
\[\mathbf{y}(\mathbf{x},\mathbf{w}) = \mathbf{W}^\text{T}\boldsymbol\phi(\mathbf{x})\]$\mathbf{y}$는 $K$차원의 열 벡터이며 $\mathbf{W}$는 $M \times K$차의 매개변수 행렬, $\boldsymbol{\phi}(\mathbf{x})$는 앞에서와 같이 $\phi_j(\mathbf{x})$를 원소로 가지는 $M$차원의 열 벡터입니다. 표적 벡터의 조건부 분포를 다음 형태의 등방 가우시안 분포로 표현해보겠습니다.
\[p(\mathbf{t}\vert\mathbf{x},\mathbf{W},\beta)=\mathcal{N}(\mathbf{t}\vert\mathbf{W}^\text{T}\boldsymbol{\phi}(\mathbf{x}),\beta^{-1}\mathbf{I}\]$\mathbf{t}_1, …, \mathbf{t}_N$의 관측값이 주어질 경우 이들을 $N \times K$차의 행렬로 합칠 수 있으며 이때 $n$번째 행은 $\mathbf{t}_n^\text{T}$로 주어집니다. 이와 비슷하게 입력 벡터들 $\mathbf{x}_1, …, \mathbf{x}_N$을 행렬 $\mathbf{X}$로 합칠 수 있습니다. 이 경우 로그 가능도 함수는 다음과 같습니다.
\[\begin{aligned} \ln p(\mathbf{T}\vert\mathbf{X},\mathbf{W},\beta) &= \sum^N_{n=1}\ln\mathcal{N}(\mathbf{t}_n\vert\mathbf{W}^\text{T}\boldsymbol\phi(\mathbf{x}_n),\beta^{-1}\mathbf{I}) \\ &= \frac{NK}2\ln\left(\frac{\beta}{2\pi}\right)-\frac\beta2\sum^N_{n=1}\Vert\mathbf{t}_n-\mathbf{W}^\text{T}\boldsymbol\phi(\mathbf{x}_n)\Vert^2 \end{aligned}\]이를 $\mathbf{W}$에 대해서 최대화하면 다음과 같습니다.
\[\mathbf{W}_\text{ML}=(\boldsymbol\Phi^\text{T}\boldsymbol\Phi)^{-1}\]위 식을 각각의 타깃 변수 $t_k$에 대해 살펴보면 다음과 같습니다.
\[\mathbf{w}_k = (\boldsymbol\Phi^\text{T}\boldsymbol\Phi)^{-1}\boldsymbol\Phi^\text{T}\mathbf{t}_k=\boldsymbol\Phi^\dagger\mathbf{t}_k\]각각의 타깃 변수들에 대한 회귀 문제들의 해는 서로 분리되어 있으며, 모든 벡터 $\mathbf{w}_k$들에 대해 공유되는 유사 역행렬 $\boldsymbol\Phi^\dagger$만 계산해 내면 됩니다.
댓글남기기