[PRML] Chapter 3. Linear Regression (3) - 베이지안 모델 비교, 증거 근사, 고정 기저 함수의 문제점

본 글은 책 ‘패턴 인식과 머신 러닝’의 국내 출판본을 바탕으로 작성되었습니다.

3.4 베이지안 모델 비교

1장에서 과적합 문제에 대해 논의했었습니다. 또한 정규화 매개변수를 결정하거나 여러 모델 중 하나를 선택하는 교차 검증법도 소개했습니다. 여기서는 베이지안 측면에서 모델 선택 문제에 대해 논의하겠습니다.

모델의 매개변숫값에 대한 점 추정을 시행하는 대신에 해당 매개변수를 바탕으로 주변화를 시행함으로써 최대 가능도 방법과 연관된 과적합 문제를 피할 수 있습니다. 이 경우 훈련 집합을 바탕으로 모델들을 직접 비교할 수 있으므로 검증 집합이 따로 필요하지 않게 되며, 여러 복잡도 매개변수들을 한 번의 훈련과정에서 동시에 결정할 수 있습니다.

주변 가능도

베이지안 관점에서의 모델 비교는 모델 선택에 있어서의 불확실성을 확률로 나타내고 여기에 확률의 법칙을 일관되게 적용합니다. $L$개의 모델 ${\mathcal{M}_i}$들을 비교한다고 가정해보겠습니다. 다항식 곡선 피팅 문제의 경우 이 분포는 입력값 $\mathbf{X}$들이 알려졌다고 간주했을 때 표적값 $\mathbf{t}$들에 대해 정의되며, 이 둘의 결합 분포로 모델을 정의하는 것도 가능합니다. 데이터들이 이 모델 중 하나로부터 만들어졌다고 가정하지만 어떤 모델로부터 만들어졌는지는 불확실합니다. 이 불확실성은 사전 분포 $p(\mathcal{M}_i)$로 표현합니다. 훈련 집합 $\mathcal{D}$가 주어졌을 때 우리는 다음의 사후 분포를 구해야합니다.

\[p(\mathcal{M}_i\vert\mathcal{D}) \propto p(\mathcal{M}_i)p(\mathcal{D}\vert\mathcal{M}_i)\]

사전 분포는 각각의 다른 모델들에 대한 우리의 선호도를 표현할 수 있도록 해줍니다. 모든 모델들이 같은 사전 확률을 가진다고 단순하게 가정해보겠습니다. 모델 증거 Model evidence $p(\mathcal{D}\vert\mathcal{M}_i)$는 각각의 서로 다른 모델들에 대한 데이터로서 보여지는 선호도를 나타내는 용어입니다. 모델 증거는 매개변수들이 주변화되어 사라진 상황에서 각 모델 공간에서의 가능도 함수이기 때문에 주변 가능도 marginal likelihood 라고도 불립니다.

\[p(t\vert\mathbf{x},\mathcal{D}) = \sum^L_{i=1}p(t\vert\mathbf{x},\mathcal{M}_i,\mathcal{D})p(\mathcal{M}_i\vert\mathcal{D})\]

위와 같이 일단 모델들의 사후 분포를 알게 되면 다음과 같이 예측 분포를 구할 수 있습니다. 이는 혼합 분포 mixture distribution의 예시입니다. 각각 개별 모델의 예측분포들을 모델들의 사후 확률로 가중 평균을 내어 종합적인 예측 분포를 구하는 것입니다.

모델 평균에 대한 간단한 근사는 가장 확률이 높은 하나의 모델을 사용해서 이 모델만을 이용해 예측하는 것입니다. 이를 모델 선택 model selection 과정이라고 합니다. 매개변수 집합 $\mathbf{w}$에 의해 결정되는 모델을 고려해보겠습니다. 이 경우 모델 증거는 다음과 같습니다.

\[p(\mathcal{D}\vert\mathcal{M}_i)=\int p(\mathcal{D}\vert\mathbf{w},\mathcal{M}_i)p(\mathbf{w}\vert\mathcal{M}_i)d\mathbf{w}\]

주변 가능도는 사전 분포로부터 랜덤하게 표본 추출한 매개변수를 바탕으로 한 모델로부터 데이터 집합 $\mathcal{D}$를 생성하게 될 확률로 정의 할 수 있습니다. 매개변수들에 대한 사후 분포를 계산할 때의 베이지안 정리의 분모에 해당하는 정규화항이 모델 증거에 해당합니다.

\[p(\mathbf{w}\vert\mathcal{D},\mathcal{M}_i)=\frac{p(\mathcal{D}\vert\mathbf{w},\mathcal{M}_i)p(\mathbf{w}\vert\mathcal{M}_i)}{p(\mathcal{D}\vert\mathcal{M}_i)}\]

매개변수들에 대한 적분을 다음과 같이 단순하게 근사해서 모델 증거에 대한 통찰을 얻을 수 있습니다. 첫 번째로 단일 매개변수 $w$를 가지는 모델에 대해 고려해 보겠습니다. 매개변수에 대한 사후 분포는 $p(\mathcal{D}\vert w)p(w)$ 에 비례합니다. 사후 분포가 가장 가능성이 높은 값 $w_\text{MAP}$ 주변에서 뾰족하게 솟아있으며 그 폭이 $\Delta w_\text{posterior}$라고 가정하면 피적분 함수의 최댓값과 정점의 폭을 곱해서 적분값의 근사치를 구할 수 있습니다. 만약 사전 분포가 $\Delta w_\text{prior}$를 폭으로 가지며 평평한 형태를 가지고 있어서 $p(w) = 1 / \Delta w_\text{prior}$라고 한단계 더 가정하면 다음을 구할 수 있습니다.

\[\begin{aligned} p(\mathcal{D}) &= \int p(\mathcal{D}\vert w)p(w)dw \simeq p(\mathcal{D}\vert w_\text{MAP})\frac{\Delta w_\text{posterior}}{\Delta w_\text{prior}} \\ \ln p(\mathcal{D}) &\simeq \ln p(\mathcal{D}\vert w_\text{MAP}) + \ln\left(\frac{\Delta w_\text{posterior}}{\Delta w_\text{prior}}\right) \end{aligned}\]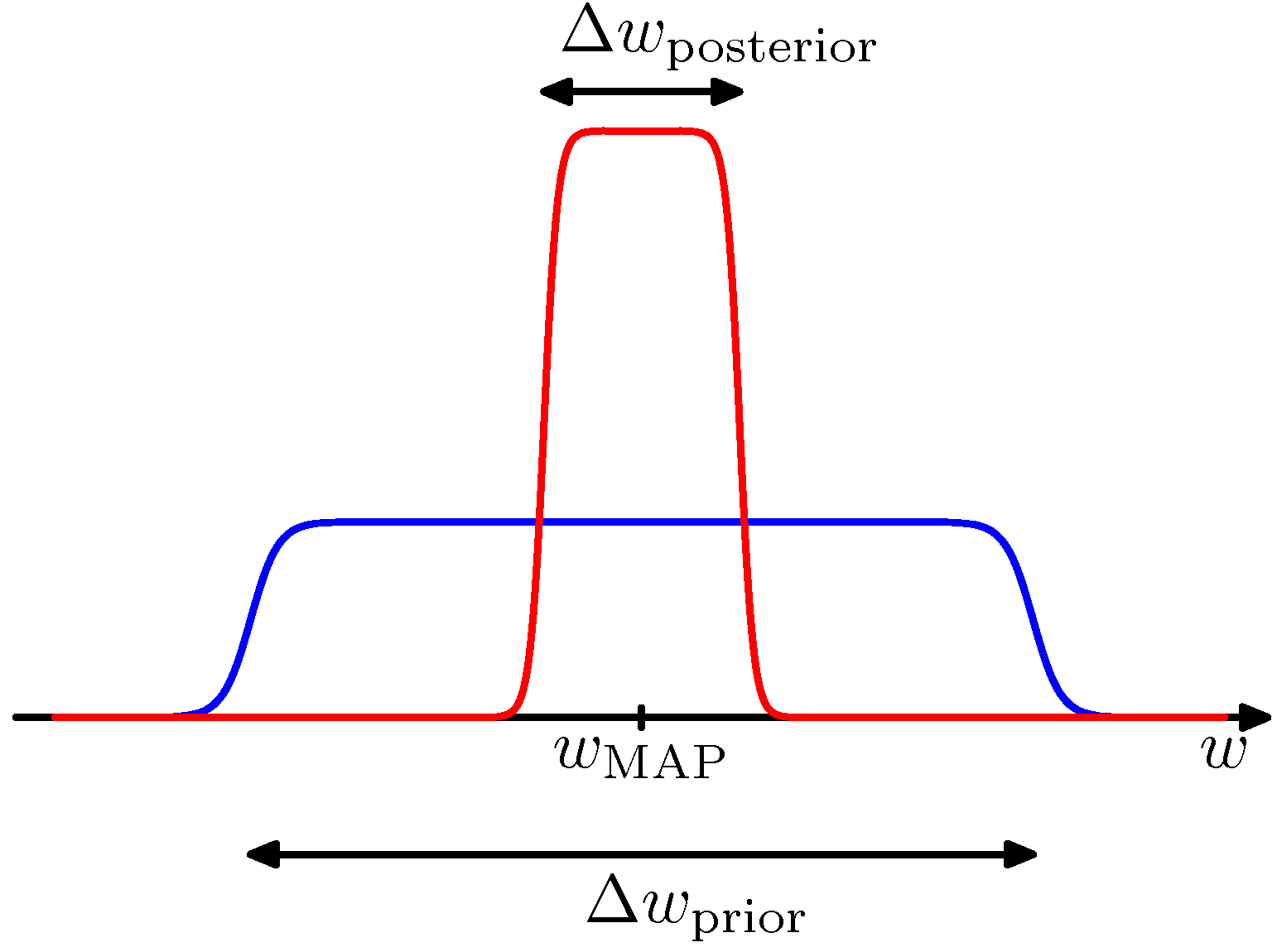

Figure 3.12 매개변수에 대한 사후 분포가 최빈값 $w_\text{MAP}$ 주변에서 솟아 있다고 가정했을 때의 분포

위 그림은 근사치를 그린 것입니다. 첫 번째 항은 가장 가능성이 높은 매개변수를 바탕으로 데이터에 근사한 것입니다. 평평한 사전 분포의 경우 로그 가능도에 해당합니다. 두 번째 항은 모델의 복잡도에 대해 벌칙을 주는 것입니다. 매개변수들이 사후 분포의 데이터들에 대해 세밀하게 조절되면 벌칙항이 더 커지게 됩니다.

$M$개의 매개변수를 가진 모델에 대해서는 비슷한 근사를 각각의 매개변수들에 대해 순서대로 시행하게 됩니다. 모든 매개변수들이 같은 $\Delta w_\text{posterior} / \Delta w_\text{prior}$ 비율을 가졌다고 가정하면 다음과 같습니다.

\[\ln p(\mathcal{D})\simeq \ln p(\mathcal{D}\vert\mathbf{w}_\text{MAP}) + M\ln\left(\frac{\Delta w_\text{posterior}}{\Delta w_\text{prior}}\right)\]

이 경우 복잡도 벌칙항의 크기는 모델의 적응 매개변수 $M$의 숫자에 따라 선형적으로 증가합니다. 대부분의 경우 더 복잡한 모델이 데이터에 더 잘 근사되기 때문에 복잡도를 증가시킴에 따라서 첫 번째 항의 크기는 보통 증가하게 되지만 두 번째 항은 감소하게 됩니다. 최대 근거에 따라 결정되는 최적의 모델 복잡도는 서로 경쟁하는 이 두 항의 균형에 따라 주어지게 됩니다.

베이지안 모델 비교

이제 밑의 그림을 바탕으로 베이지안 모델 비교에 대해 살펴보겠습니다.

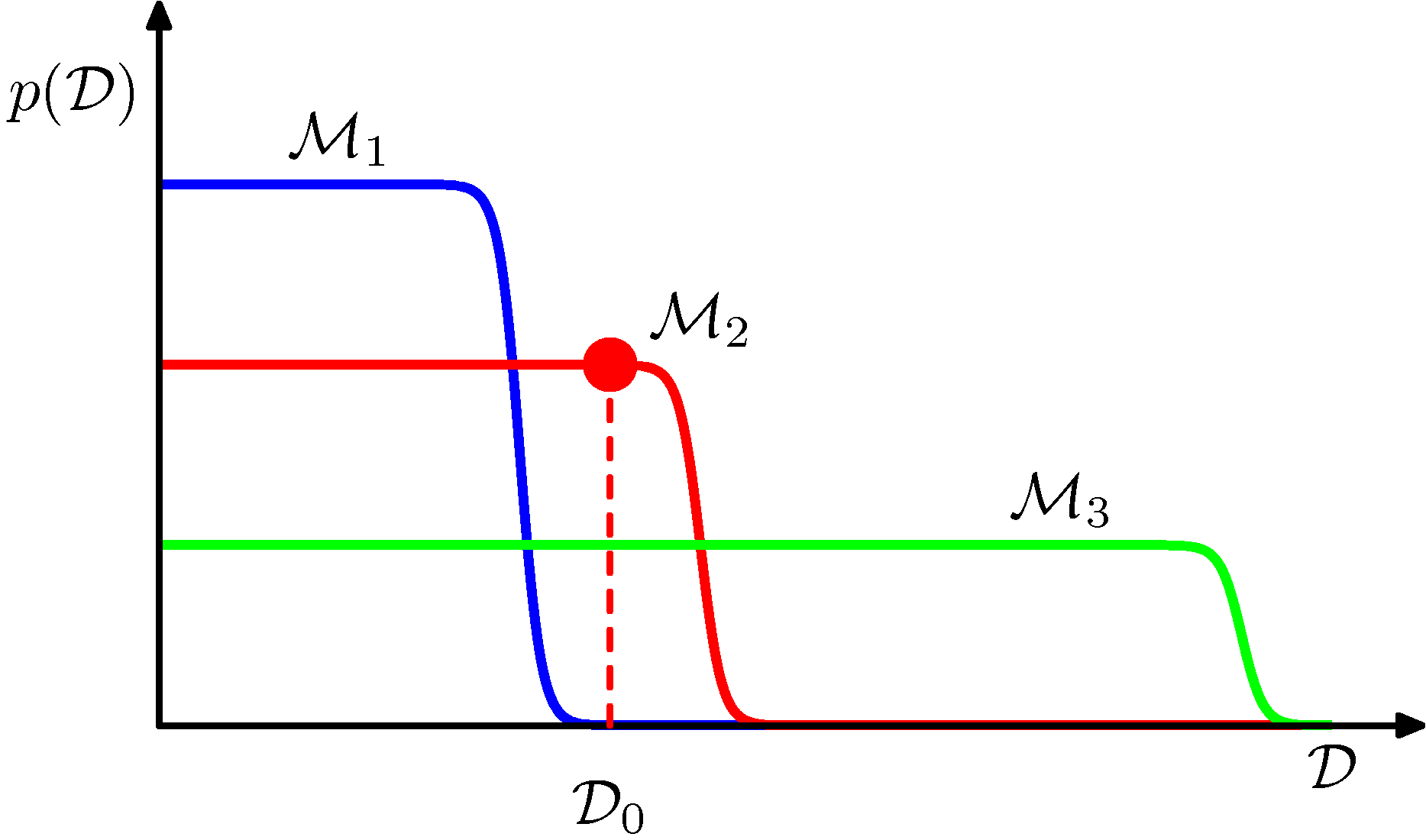
Figure 3.13 서로 다른 복잡도를 가지는 세 모델에서의 데이터 집합의 분포

가로측은 가능한 데이터 집합들의 공간에 대한 일차원 표현이며, 각각의 점은 특정 데이터 집합을 의미합니다. 순서대로 복잡도가 증가하는 세 개의 모델 $\mathcal{M}_1, \mathcal{M}_2, \mathcal{M}_3$를 고려해 보겠습니다. 이 모델들을 활용하여 예시 데이터 집합을 만들고 그 분포를 살펴본다고 한다면, 어떤 모델이든 다양한 서로 다른 데이터 집합을 생성할 수 있습니다. 특정 모델로부터 특정 데이터 집합을 만들어 내기 위해서는 첫 번째로 사전 분포 $p(\mathbf{w})$로부터 매개변숫값을 선택하고, 두 번째로 이 매개변수를 바탕으로 한 $p(\mathcal{D}\vert\mathbf{w})$로부터 데이터를 추출해야 합니다. 단순한 모델은 생성된 데이터 집합 간의 차이가 작고 복잡한 모델일 수록 다양한 종류의 데이터 집합이 생성될 것입니다. $p(\mathcal{D}\vert \mathcal{M}_i)$는 정규화되어 있기 때문에 특정 데이터 집합 $\mathcal{D}_0$는 중간 정도의 복잡도를 가진 모델에 대해서 가장 큰 증것값을 가지게 됩니다. 단순한 모델은 데이터에 잘 근사하지 못 하지만 복잡한 모델은 예측 확률을 너무 넓은 데이터 집합들에 대해 퍼뜨려 각각의 데이터 집합들에 대해 작은 확률을 할당하게 됩니다.

가정

베이지안 모델 비교 방법은 데이터가 생성된 원래의 분포가 현재 고려하고 있는 모델 집합에 포함되어 있다는 것을 암시적으로 내포하고 있습니다. 이것이 사실이라면 베이지안 모델 비교법은 평균적으로 올바른 모델을 선택한다는 것을 증명할 수 있습니다.

증명

모델 $\mathcal{M}_1$과 $\mathcal{M}_2$를 고려하고 원 모델은 $\mathcal{M}_1$이라고 해보겠습니다. 주어진 제한된 크기의 데이터 집합에 대해서는 틀린 모델에 대한 베이즈 요인이 더 클 수도 있지만 베이즈 요인을 데이터 집합의 분포에 대해 평균을 내면 다음과 같습니다.

\[\int p(\mathcal{D}\vert\mathcal{M}_1)\ln\frac{p(\mathcal{D}\vert\mathcal{M}_1)}{p(\mathcal{D}\vert\mathcal{M}_2)}d\mathcal{D}\]

여기서 평균값은 데이터의 실제 분포에 대해 계산되었습니다. 이 수치는 쿨백 라이블러 발산 Kullback-Leibler divergence의 예시이며 두 분포가 일치해서 0 값을 가질 때를 제외하면 항상 양의 값을 가집니다. 따라서 평균적으로 베이즈 요인은 올바른 모델을 선택하게 됩니다.

정리

지금까지 베이지안 방법론을 사용해서 훈련 집합만을 이용해서 과적합 문제를 피하고 모델을 비교할 수 있다는 것을 살펴보았습니다. 하지만 베이지안 방법론 역시 모델의 형태에 대한 가정을 해야하며, 가정이 틀렸다면 결과값 역시 매우 틀릴 수 있습니다. 모델 증거는 사전 분포의 많은 측면들에 대해 민감합니다. 분포의 꼬리 부분에서의 작용이 그 예시입니다. 따라서 실제 응용 사례에서는 독립적인 시험 집합을 따로 빼놓고 최종적으로 전체 시스템의 성능을 확인하는 것이 좋습니다.

3.5 증거 근사

완전 베이지안 관점을 바탕으로 한 선형 기저 함수 모델에 대해 논의해 보겠습니다. 초매개변수 $\alpha$와 $\beta$에 대한 사전 분포를 도입하고 초매개변수들과 $\mathbf{w}$에 대해 주변화를 통해서 예측을 시행할 것입니다. $\mathbf{w}$나 초매개변수들에 대해 적분하는 것은 변수들 모두에 대해 완벽한 주변화를 하는 것이 해석적으로 불가능에 가까우므로 여기서는 매개변수의 주변 가능도 함수 marginal likelihood function을 극대화하여 결정되는 값으로 초매개변수를 설정하는 근사법을 사용할 것입니다. 이때 매개변수의 주변 가능도 함수는 매개변수 $\mathbf{w}$에 대한 적분을 통해 구할 수 있습니다. 머신러닝 문헌들에서는 이를 증거 근사 evidence approximation 이라고 부르기도 합니다.

$\alpha$와 $\beta$에 대한 초사전 분포를 도입하면 $\mathbf{w}, \alpha, \beta$에 대한 주변화를 통해 예측 분포를 구할 수 있습니다

\[p(t\vert\mathbf{t}) = \int\int\int p(t\vert\mathbf{w},\beta)p(\mathbf{w}\vert\mathbf{t},\alpha,\beta)p(\alpha,\beta\vert\mathbf{t})d\mathbf{w}d\alpha d\beta\]

베이지안 정리에 따라서 $\alpha$와 $\beta$에 대한 사후 분포는 다음과 같이 주어집니다.

\[p(\alpha,\beta\vert\mathbf{t})\propto p(\mathbf{t}\vert\alpha,\beta)p(\alpha,\beta)\]

만약 사전 분포가 상대적으로 평평하다면 증거 방법론에서 $\widehat\alpha, \widehat\beta$의 값은 주변 가능도 함수 $p(\mathbf{t}\vert\alpha,\beta)$를 최대화함으로써 구할 수 있습니다. 선형 기저 함수 모델의 주변 가능도 함수를 구하고 그 최댓값을 찾는 방식으로 진행한다면 교차 검증법을 사용할 필요 없이 훈련 집합 데이터만으로 초매개변수들의 값을 결정할 수 있습니다.

로그 증것값을 극대화하는 데는 두 가지 방법이 있습니다. 첫 번째 방법은 증거 함수를 해석적으로 계산하고 그 미분값을 0으로 설정하여 $\alpha, \beta$에 대한 재추정 공식을 구하는 것입니다. 두 번째 방법은 EM 알고리즘을 적용하는 것입니다. 여기서는 첫 번째 방법을 살펴보겠습니다.

증거 함수 계산

가중 매개변수 $\mathbf{w}$에 대해서 적분해서 주변 가능도 함수 $p(\mathbf{t}\vert\alpha,\beta)$를 구할 수 있습니다.

\[\begin{aligned} p(\mathbf{t}\vert\alpha,\beta) &= \int p(\mathbf{t}\vert\mathbf{w},\beta)p(\mathbf{w}\vert\alpha)d\mathbf{w} \\ &= \left(\frac{\beta}{2\pi}\right)^{N/2}\left(\frac\alpha{2\pi}\right)^{M/2}\int\exp\{-E(\mathbf{w})\}d\mathbf{w} \end{aligned}\]

$M$은 $\mathbf{w}$의 차원수입니다. 또한 $E(\mathbf{w})$는 다음과 같습니다.

\[\begin{aligned} E(\mathbf{w}) &= \beta E_D(\mathbf{w}) + \alpha E_W(\mathbf{w}) \\ &= \frac\beta2\Vert\mathbf{t}-\boldsymbol\Phi\mathbf{w}\Vert^2+\frac\alpha2\mathbf{w}^\text{T}\mathbf{w} \end{aligned}\]

위 식에서 $\mathbf{w}$에 대해 제곱식의 완성 방식을 적용하면 다음과 같습니다.

\[E(\mathbf{w}) = E(\mathbf{m}_N) + \frac12(\mathbf{w}-\mathbf{m}_N)^\text{T}\mathbf{A}(\mathbf{w}-\mathbf{m}_N)\]

여기서 다음을 사용하였습니다.

\[\begin{aligned} \mathbf{A} &= \alpha\mathbf{I} + \beta\boldsymbol\Phi^\text{T}\boldsymbol\Phi \\ E(\mathbf{m}_N) &= \frac\beta2\Vert\mathbf{t}-\boldsymbol\Phi\mathbf{m}_N\Vert+\frac\alpha2\mathbf{m}^\text{T}_N\mathbf{m}_N \end{aligned}\]

$\mathbf{A}$는 오류 함수의 이차 미분값에 해당합니다.

\[\mathbf{A} = \nabla\nabla E(\mathbf{w})\]

$\mathbf{A}$를 헤시안 행렬 Hessian matrix라고 합니다. 여기서 또한 $\mathbf{m}_N$은 다음과 같습니다.

\[\mathbf{m}_N = \beta\mathbf{A}^{-1}\boldsymbol\Phi^\text{T}\mathbf{t}\]

$\mathbf{A} = \mathbf{S}^{-1}_N$이므로 사후 분분포의 평균을 나타내는 식임을 알 수 있습니다.

이제 다변량 가우시안의 정규화 계수에 대한 표준 결과를 바탕으로 $\mathbf{w}$에 대한 적분을 시행할 수 있습니다.

\[\int\exp\{-E(\mathbf{w})\}d\mathbf{w} = \exp\{-E(\mathbf{m}_N)\}(2\pi)^{M/2}\vert\mathbf{A}\vert^{-1/2}\]

또 주변 가능도에 로그를 취한 식을 다음의 형태로 적을 수 있습니다.

\[\ln p(\mathbf{t}\vert\alpha,\beta) = \frac M2\ln\alpha + \frac N2 \ln \beta - E(\mathbf{m}_N) -\frac12\ln\vert\mathbf{A}\vert-\frac N2\ln(2\pi)\]

위 식은 증거 함수에 필요한 표현식입니다.

피팅 결과 문제로 돌아가서 다항식의 차수에 대한 모델 증거를 다음과 같이 그려보도록 하겠습니다.

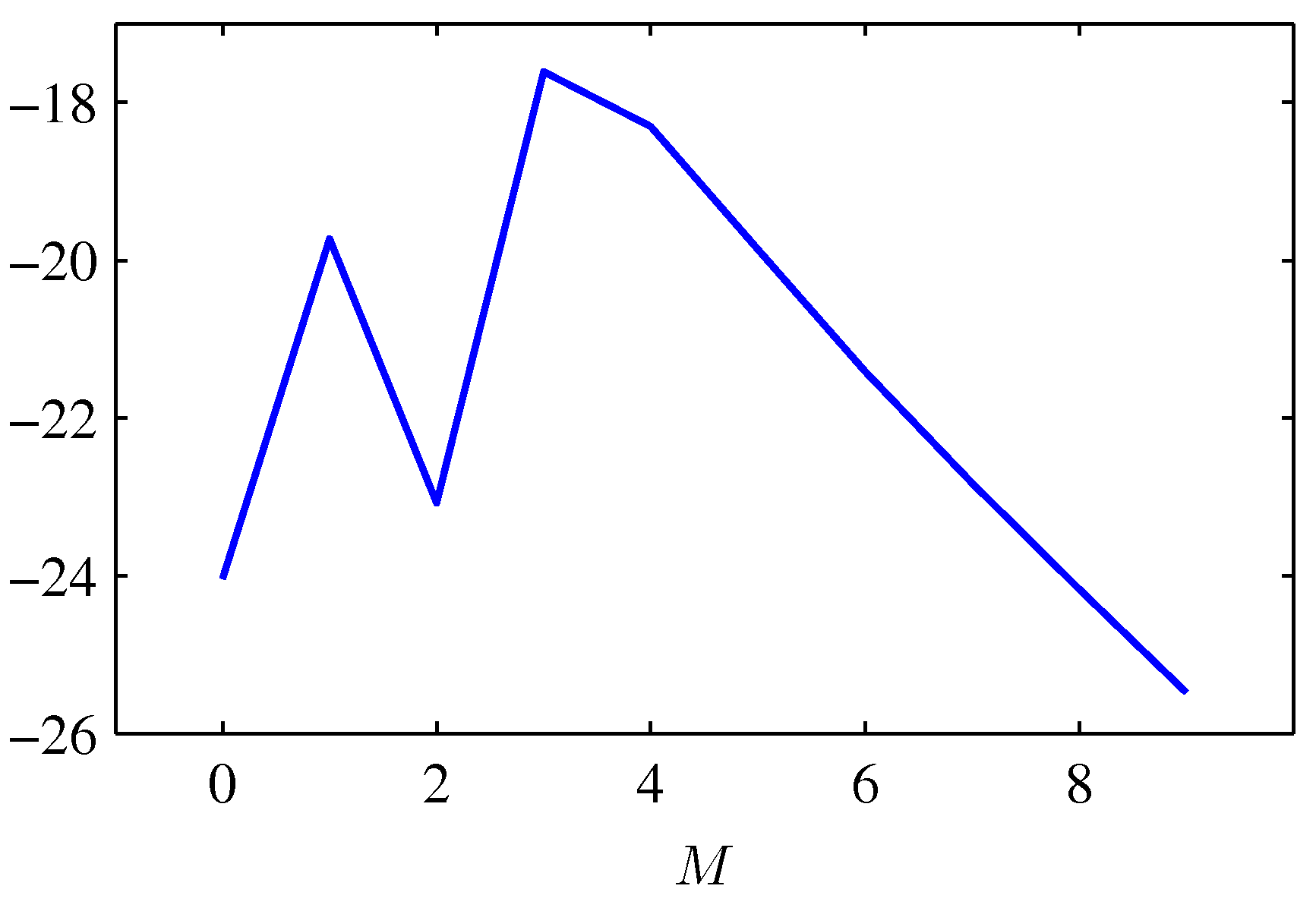
Figure 3.14 다항 회귀 모델의 차수 $M$과 그에 따른 로그 증것값

$M=0$인 다항식은 데이터에 대해 잘 피팅되지 않았으며 상대적으로 낮은 증것값을 가집니다. $M=1$ 다항식의 경우 근사가 매우 개선되며 증것값 역시 상당히 커집니다. $M=2$인 경우 데이터 근사가 아주 조금 개선되는데 데이터를 생성한 기저의 사인 곡선 함수가 홀함수이기 때문입니다. $M=3$이 되면 피팅이 상당히 향상되고 증것값도 증가합니다. 결과적으로 $M=3$인 경우 가장 좋은 증것값을 가지게 됩니다. 이보다 $M$이 더 커질 경우 모델의 복잡도가 증가해 벌칙값이 커지므로 전체 증것값은 감소합니다.

증거 함수 극대화

$p(\mathbf{t}\vert\alpha,\beta)$를 $\alpha$에 대해 극대화하는 것을 고려해보겠습니다. 이를 위해 고유 벡터 방정식을 정의하겠습니다.

\[(\beta\boldsymbol\Phi^\text{T}\boldsymbol\Phi)\mathbf{u}_i = \lambda_i\mathbf{u}_i\]

위 식으로부터 $\mathbf{A}$가 고윳값 $\alpha + \lambda_i$를 가짐을 알 수 있습니다. 이제 위에서 봤던 로그 주변 가능도 함수 표현식의 $\ln\vert\mathbf{A}\vert$항을 $\alpha$에 대해 미분하는 것을 고려해 보겠습니다.

\[\frac d{d\alpha}\ln\vert\mathbf{A}\vert=\frac d{d\alpha}\ln\prod_i(\lambda_i+\alpha)=\frac d{d\alpha}\sum_i\ln(\lambda_i+\alpha)=\sum_i\frac1{\lambda_i+\alpha}\]

따라서 $\alpha$에 대한 정륫값들은 다음을 만족하게 됩니다.

\[\begin{aligned} 0 &= \frac M{2\alpha}-\frac12\mathbf{m}^\text{T}_N\mathbf{m}_N-\frac12\sum_i\frac1{\lambda_i+\alpha} \\ \alpha\mathbf{m}^\text{T}_N\mathbf{m}_N &= M - \alpha\sum_i\frac1{\lambda_i + \alpha} = \gamma \\ \gamma &= \sum_i\frac{\lambda_i}{\alpha + \lambda_i} \end{aligned}\]

$\gamma$ 값이 의미하는 바는 잠시 후에 살펴보겠습니다. 위 식으로부터 주변 가능도 함수를 극대화하는 $\alpha$ 값이 다음과 같음을 알 수 있습니다.

\[\alpha = \frac\gamma{\mathbf{m}^\text{T}_N\mathbf{m}_N}\]

$\gamma$ 값은 $\alpha$에 종속적이며 사후 분포의 최빈값 $\mathbf{m}_N$ 또한 $\alpha$의 선택에 따라 종속적입니다. 따라서 이는 암시적인 해이며 반복적 과정을 적용해야 합니다. 초기 $\alpha$값을 결정하고 이를 통해 $\mathbf{m}_N$을 구하고 $\gamma$값을 구한 뒤 다시 $\alpha$값을 추정하는 데 사용하는 과정을 $\alpha$값이 수렴할 때까지 반복합니다. 행렬 $\boldsymbol\Phi^\text{T}\boldsymbol\Phi$값은 고정되어 있기 때문에 이 행렬의 고윳값을 계산한 후 여기에 $\beta$를 곱하면 $\lambda_i$값을 구할 수 있습니다. 이를 통해 오직 훈련 데이터만을 사용하여 $\alpha$ 값을 구할 수 있습니다. 모델의 복잡도를 최적화하는 데 있어서 다른 데이터 집합이 필요하지 않습니다.

비슷한 방법으로 로그 주변 가능도 함수를 $\beta$에 대해서도 극대화할 수 있스빈다. 고윳값 $\lambda_i$는 $\beta$에 대해 비례하기 때문에 $d\lambda_i/d\beta = \lambda_i/\beta$ 임을 이용할 수 있습니다.

\[\frac d{d\beta} = \ln\vert\mathbf{A}\vert = \frac d{d\beta}\sum_i\ln(\lambda_i + \alpha) = \frac1\beta\sum_i\frac{\lambda_i}{\lambda_i + \alpha} = \frac\gamma\beta\]

따라서 주변 가능도의 임계점은 다음을 만족시킵니다.

\[0 = \frac{N}{2\beta} - \frac12\sum^N_{n=1}\left\{t_n-\mathbf{m}^\text{T}_n\boldsymbol\phi(\mathbf{x}_n)\right\}^2 - \frac\gamma{2\beta}\] \[\frac1\beta = \frac1{N-\gamma}\sum^N_{n=1}\left\{t_n-\mathbf{m}^\text{T}_N\boldsymbol\phi(\mathbf{x}_n)\right\}^2\]

$\beta$에 대한 내재적 해이므로 $\alpha$와 같은 방식으로 수렴할 때까지 반복할 수 있습니다.

유효 매개변수의 숫자

위에서 살펴본 $\alpha$를 극대화하는 식을 다음과 같이 해석하면 $\alpha$의 베이지안 해에 대한 통찰을 얻을 수 있습니다.

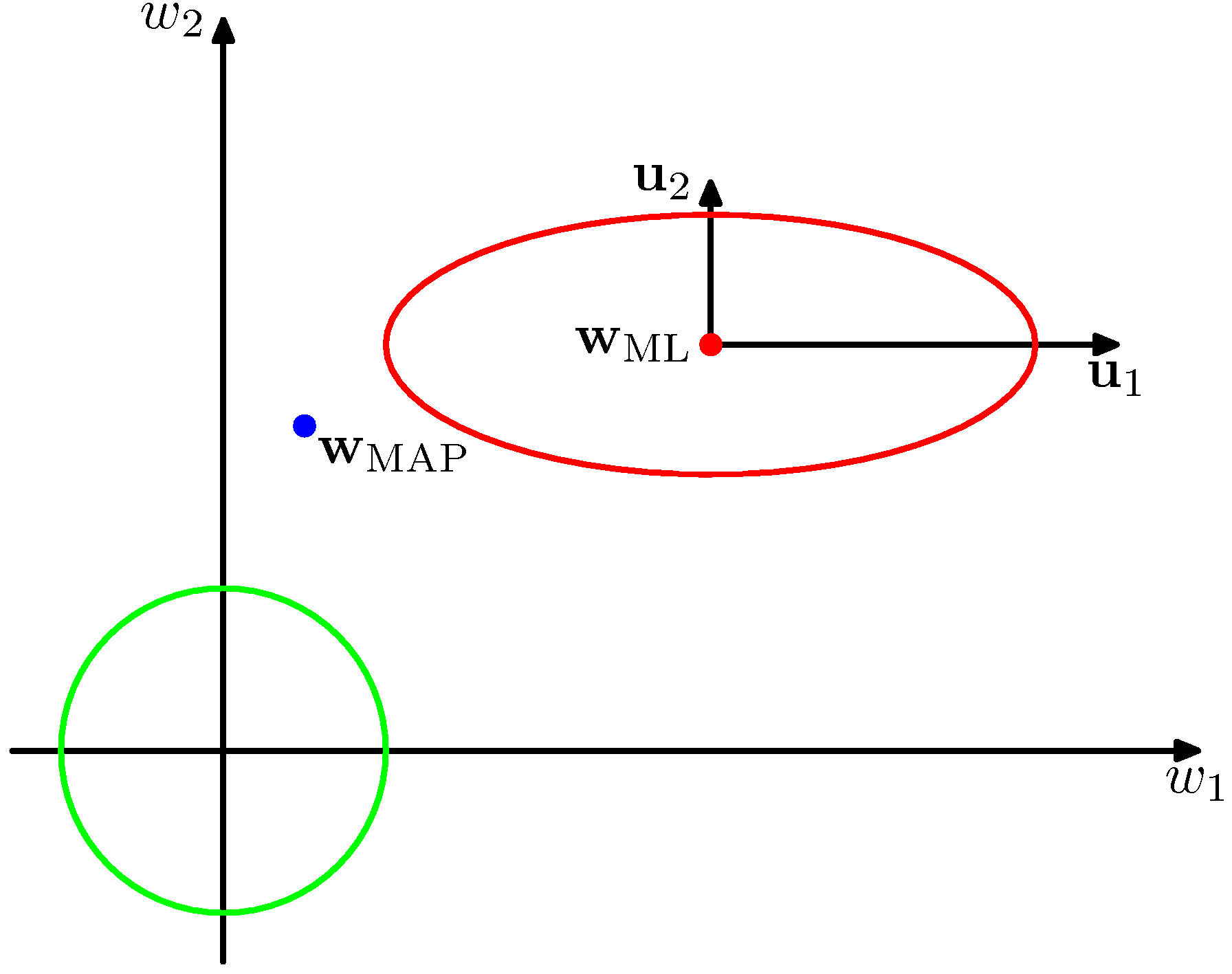
Figure 3.15 가능도 함수의 윤곽선(빨강)과 사전 분포의 윤곽선(녹색)

위 그림에서는 암시적으로 회전 변환을 시행해서 공간의 축이 고유 벡터 $\mathbf{u}_i$에 대해 정렬되도록 하였습니다. 여기서 고윳값 $\lambda_i$는 가능도 함수의 곡률을 결정합니다. 고윳값 $\lambda_1$은 고윳값 $\lambda_2$보다 작은데, 곡률값이 작을수록 윤곽선이 해당 방향으로 더 길게 자리하기 때문입니다.

$\beta\boldsymbol\Phi^\text{T}\boldsymbol\Phi$는 양의 정부호 행렬이기 때문에 양의 고윳값을 가지며 따라서 $\lambda_i/(\lambda_i + \alpha)$는 0과 1 사이의 값을 가집니다. $\gamma$는 $0 \leq \gamma \leq M$의 범위 상에 존재하게 되며 $\lambda_i \gg \alpha$ 방향의 경우 이에 해당하는 매개변수 $w_i$는 최대 가능도에 가깝게 되며 $\lambda_i/(\lambda_i + \alpha)$는 1에 가깝게 됩니다. 이러한 매개변수는 데이터에 의해 밀접하게 제약되기 때문에 잘 결정된 well determined 매개변수라고 합니다. 반대로 $\lambda_i \ll \alpha$의 경우 매개변수 $w_i$는 0에 가깝게 되고 $\lambda_i/(\lambda_i + \alpha)$도 0에 가깝게 되빈다. 이런 경우 가능도 함수가 상대적으로 매개변숫값에 대해 덜 민감하며 그렇기 때문에 사전 분포에 의해 매개변숫값이 더 작게 설정됩니다. 따라서 $\gamma$는 잘 결정된 매개변수의 유효 숫자를 측정하는 값에 해당하게 됩니다.

$\beta$를 재추정하는 데 쓰이는 식과 그에 해당하는 식의 최대 가능도 결과를 비교해보면 약간의 통찰을 얻을 수 있습니다. 두 식은 표적값과 모델 예측값의 차이의 제곱을 평균낸 것으로 분산을 표현합니다. 하지만 이 두 식 사이에는 최대 가능도 결과에서의 부놈의 값인 데이터의 개수 $N$이 베이지안 결과에서는 $N - \gamma$로 바뀌었습니다.

앞서 단일 변수 $x$에 대한 가우시안 분포 분산의 최대 가능도 추정값을 다음과 같이 구했습니다.

\[\sigma^2_\text{ML}=\frac1N\sum^N_{n=1}(x_n-\mu_{ML})^2\]

이 추정값은 최대 가능도 해 $\mu_\text{ML}$이 데이터상의 노이즈에 대해서도 피팅되어 있기 때문에 편향되어 있습니다. 비편향 추정값은 다음과 같습니다.

\[\sigma^2_\text{MAP}=\frac1{N-1}\sum^N_{n=1}(x_n-\mu_\text{ML})^2\]

베이지안 결괏값의 분모 인자 $N-1$은 하나의 자유도가 평균값을 근사하는 데 사용되었음을 고려하여 결정됐습니다. 이 인자를 사용함으로써 최대 가능도에서의 편향이 사라집니다. 이제는 이 결과를 선형 회귀 모델상에서 살펴보겠습니다. 이제 표적 분포의 평균은 $M$개의 매개변수를 포함하고 있는 $\mathbf{w}^\text{T}\boldsymbol\phi(\mathbf{x})$로 주어집니다. 데이터에 의해 결정된 유효한 매개변수의 숫자는 $\gamma$이며 나머지 $N-\gamma$의 매개변수들은 사전 분포에 의해 작은 값으로 설정되었습니다.

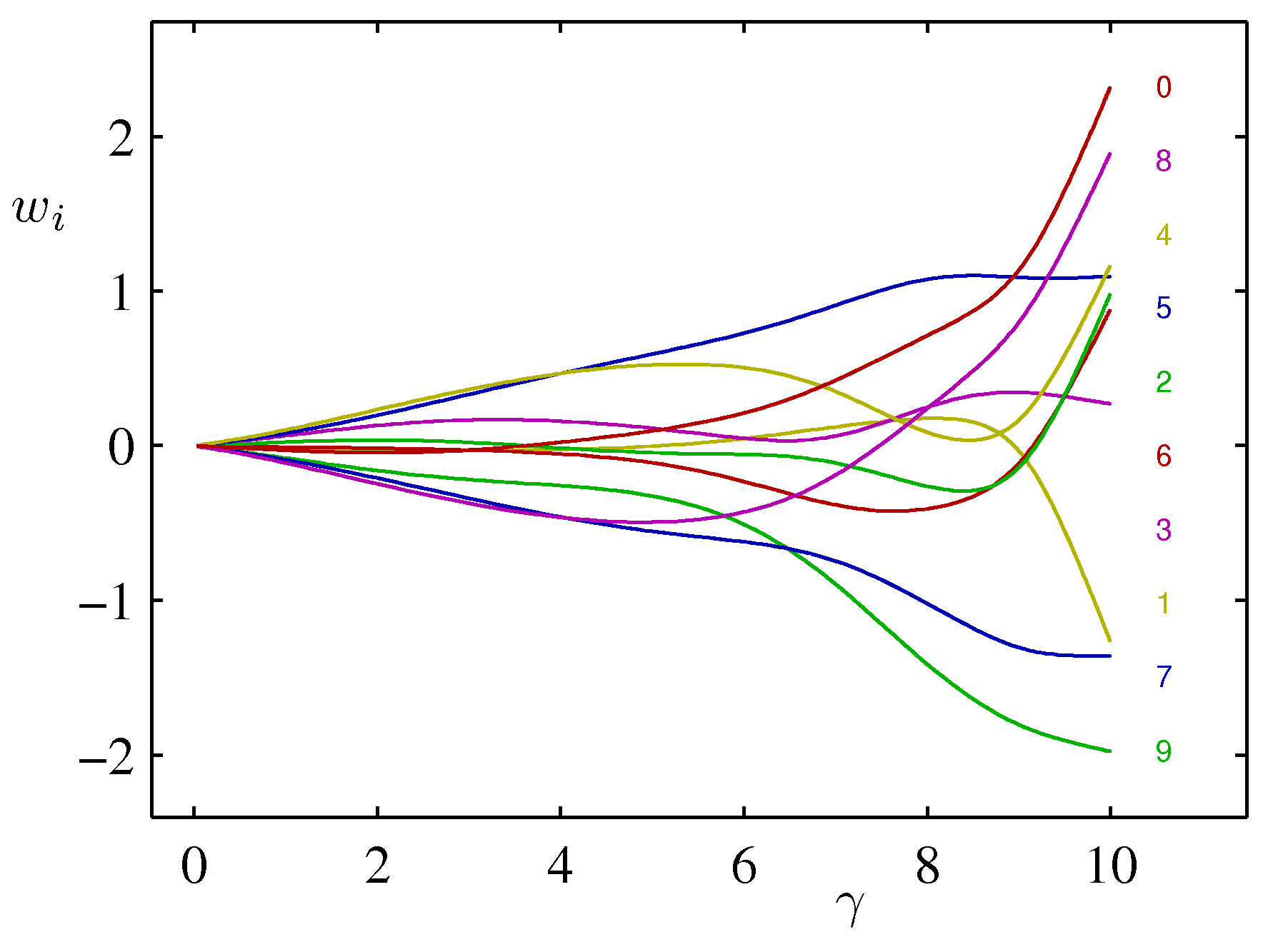
Figure 3.17 매개변수의 유효 숫자 $\gamma$와 각 개별 매개변수들 간의 도식

데이터의 숫자 $N$이 매개변수의 숫자 $M$보다 큰 $N \gg M$의 경우를 고려해 보겠습니다. 이 경우 모든 매개변수들은 데이터로부터 잘 결정될 수 있다는 것을 알 수 있습니다. $\boldsymbol\Phi^\text{T}\boldsymbol\Phi$는 데이터들에 대한 내재적인 합산을 포함하고 있으며 따라서 데이터 집합의 크기가 증가함에 따라서 고윳값 $\lambda_i$들의 크기가 증가하기 때문입니다. 이 경우 $\gamma = M$이며 $\alpha, \beta$에 대한 재추정 공식은 다음과 같습니다.

\[\begin{aligned} \alpha &= \frac{M}{2E_W(\mathbf{m}_N)} \\ \beta &= \frac{N}{2E_D(\mathbf{m}_N)} \end{aligned}\]

이 결괏값들을 완전 증거 재추정에 대한 계산하기 쉬운 근삿값으로 사용할 수 있습니다. 이 결괏값들의 경우에는 헤시안 행렬의 고윳값 스펙트럼을 계산할 필요가 없기 때문입니다.

3.6 고정 기저 함수의 한계점

이 장 전반에 걸쳐 고정된 비선형 기저 함수들의 선형 결합으로 이루어진 모델을 살펴보았습니다. 매개변수들의 선형성을 가정할 경우에 최소 제곱 문제의 해가 닫힌 형태로 존재하며, 베이지안 과정을 통해서 풀이가 가능하다는 장점이 있습니다. 또 기저 함수를 적절히 선택할 경우 입력 변수와 타깃 변수 사이의 임의의 비선형성도 모델할 수 있습니다.

하지만 선형 모델에는 심각한 한계가 있습니다. 기저 함수 $\phi_j(\mathbf{x})$가 훈련 데이터 집합이 관측되기 전에 고정되어 있으며 이에 따라서 차원의 저주 문제의 징후를 보입니다. 선형 모델의 경우 기저 함수의 숫자는 입력 공간 차원 $D$가 증가함에 따라 아주 빠르게 증가합니다.

이러한 문제를 완화하기 위해 데이터 집합의 두 가지 성질을 이용할 수 있습니다. 첫번째로 데이터 벡터들 ${\mathbf{x}_n}$은 보통 내재적 차원수가 입력 공간의 차원수보다 작은 비선형 매니폴드에 근접하게 존재합니다. 그 결과 입력 변수들 사이에 강한 상관관계가 존재합니다. 만약 우리가 지역화된 기저 함수를 사용한다면 입력 공간상에서 데이터를 포함하는 지역에만 이 기저 함수들이 퍼져 있도록 배열할 수 있습니다. 시그모이드 sigmoid 비선형성을 가진 적응적 기저 함수를 사용하는 뉴럴 네트워크 모델의 경우 기저 함수가 달라지는 입력 공간 상의 지역들이 데이터 매니폴드에 해당하도록 매개변수를 조절하는 방식을 사용할 수 있습니다. 두 번째 성질은 타깃 변수들이 데이터 매니폴드의 몇몇 일부 방향성에 대해서만 중요한 종속성을 가졌을 수 있다는 점입니다. 뉴럴 네트워크 모델의 경우 기저함수가 반응하는 입력 공간의 방향성을 선택하는 방식으로 이 성질을 사용합니다.