[Paper Review] Image-to-Image Translation with Conditional Adversarial Networks

Reference

Image-to-Image Translation with Conditional Adversarial Networks

Phillip Isola, Jun-Yan Zhu, Tinghui Zhou, Alexei A. Efros

IEEE, 2016.

https://arxiv.org/abs/1611.07004

0. Abstract

Conditional adversarial networks를 일반화된 Image-to-Image 문제에 적용했습니다. Input-Output 맵핑 뿐만 아니라 맵핑을 훈련할 때의 손실 함수도 학습할 수 있습니다. 따라서 전통적으로 매우 다른 형태의 손실 공식을 필요로 하던 문제들에도 이러한 일반화 된 접근 방식을 적용할 수 있습니다. 이 논문에서는 라벨과 그림의 동기화, 경계선으로부터 이미지 복원, 흑백 이미지에 색칠하기 등의 작업을 효과적으로 해냈음을 보입니다.

1. Introduction

기존에는 많은 이미지 작업들이 따로따로 연구되어 왔습니다. 이 논문에서는 이러한 다양한 종류의 변환 문제를 위한 일반적인 framework를 제시하고자 합니다.

CNN도 이러한 맥락에서 좋은 성과를 거두고 있습니다. CNN은 손실 함수를 최소화하는 방향으로 학습합니다. 하지만 우리가 무엇을 최소화해야 하는지는 직접 설정해줘야하는 문제가 있습니다. 가령 결과와 정답 사이의 유클리드 거리를 최소화하도록 한다면 흐린 이미지를 생성합니다.

만약 원하는 것을 고수준의 목표로 말할 수 있다면 네트워크는 스스로 그러한 목표에 맞게 loss를 줄여나갈 것이며, GAN이 바로 이를 성공적으로 수행하는 모델입니다. GAN은 실제와 가짜를 구분하지 못 하도록 학습이 진행되며 따라서 흐린 이미지를 생성하지 않습니다.

이 논문에서는 CGAN이라는 조건부 생성 모델을 사용합니다. Conditional GAN이 넓은 범위의 문제에서 충분히 좋은 결과를 가져다준다는 것을 밝히고, 이를 위한 framework를 제안하고 여러 중요한 아키텍쳐의 효과를 분석합니다.

2. Method

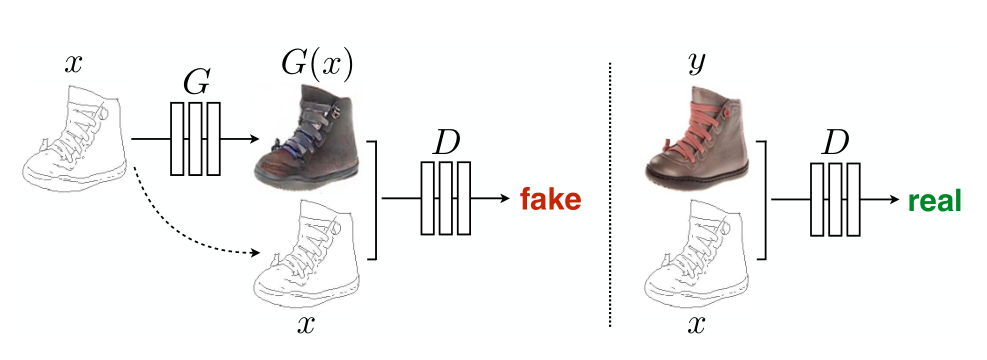
Figure 1. CGAN

GAN은 random noise vector $z$로부터 output image $y$를 생성하는 $G : z \rightarrow y$를 학습하는 생성모델입니다. 이에 더해서 CGAN은 $z$와 observed image $x$로부터 $y$로의 mapping인 $G : x,z \rightarrow y$를 학습합니다.

2.1 Objective

CGAN의 목적함수는 다음과 같습니다.

\[\mathcal{L}_{\text{cGAN}}(G,D) = \mathbb{E}_{x,y}[\log D(x,y)]+\mathbb{E}_{x,z}[\log(1-D(G(X,z)))]\]

이때 $D$를 조건부로 설정하는 것의 중요성을 살펴보기 위해, $D$가 $x$를 관측하지 못 할때의 uncoditinal variant도 비교했습니다.

\[\mathcal{L}_{\text{GAN}}(G,D) = \mathbb{E}_{y}[\log D(y)]+\mathbb{E}_{x,z}[\log(1-D(G(X,z)))]\]

여기서 GAN의 목적을 L1과 같은 전통적인 손실을 섞는 것이 효과적이라는 것을 발견했습니다. $D$의 역할은 변하지 않지만 $G$는 $D$를 속이는 것 뿐만 아니라 실제값과 가까워져야 하기 때문입니다.

\[\mathcal{L}_{L1}(G) = \mathbb{E}_{x,y,z}[\Vert y-G(x,z)\Vert_1]\]

따라서 최종적인 Objective는 다음과 같습니다.

\[G^* = \arg\min_G\max_D\mathcal{L}_{\text{cGAN}}(G,D) + \lambda\mathcal{L}_{L1}(G)\]

네트워크는 $z$가 없어도 $x$에서 $y$로 향하는 맵핑을 학습할 수 있습니다. 하지만 결과론적인deterministic 결과를 생성하게 되어 델타 함수가 아닌 다른 분포에 대해서는 제대로 된 결과를 보여주지 않습니다. 이전의 conditional GAN에서는 가우시안 노이즈 $z$를 $G$의 입력값 $x$에 추가했습니다.

이것이 별로 효과적이지 않습니다. 네트워크는 그저 노이즈를 무시하도록 학습될 뿐입니다. 대신 dropout 시에만 노이즈를 추가하여 학습과 테스트 시 모두에 $G$의 여러 레이어에 적용되도록 했습니다. 그럼에도 불구하고 네트워크의 출력에서 아주 조금의 stochasticity만 찾을 수 있었습니다. Conditional GAN을 설계할 때에는 충분한 stochasticity를 부여해서 조건부 분포의 full entropy를 포착하는 것은 매우 중요한 과제로 남아있습니다.

2.2 Network architecture

DCGAN의 convolution-BatchNorm-Relu 모델을 기본으로 사용하였습니다.

2.2.1 Generator with skips

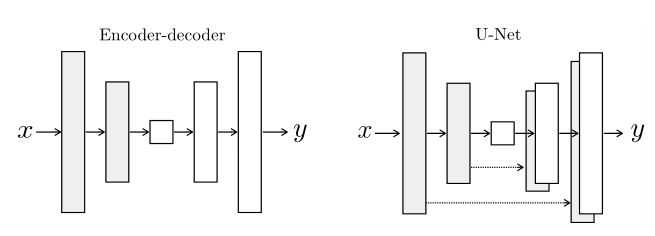
Figure 2. Generator with skips

이미지 변환 문제에서 어려운 점은 고해상도 input grid를 고해상도 output grid로 맵핑하는 것입니다. 더해서 각각의 surface appearance는 서로 다르지만 같은 underlying structure를 지닌 경우에 대해서도 고려해야 합니다.

여태까지의 연구들은 encoder-decoder 네트워크를 사용합니다. 이러한 네트워크는 bottleneck 레이어를 통과하기 때문에 정보의 손실이 필연적으로 발생합니다. 많은 image translation 문제에서는 입력과 출력 사이에서 공유되는 낮은 레벨의 정보를 잘 전달하는 것이 중요합니다.

따라서 skip-connection을 추가한 U-Net이라는 구조를 사용했습니다. 구체적으로, 전체 레이어의 갯수가 $n$이라고 할 때 $i$ 층과 $n-i$층 사이에 skip connection을 추가했습니다. 자세한 것은 위의 Figure 2를 참고해주세요.

2.2.2 Markovian discriminator (PatchGAN)

단순히 L1 손실을 추가하는 것만으로는 high-frequency를 모델링하는 것이 어렵습니다. 이를 위해서는 우리가 집중할 부분을 local image patch 단위로 제한했습니다. 구체적으로, $D$의 아키텍쳐를 $N \times N$ 크기의 patch의 단위에서 진짜인지 가짜인지 판별하도록 했으며, 이를 PatchGAN이라고 명명했습니다.

실험 단계에서 $N$이 작아도 전체 이미지를 한번에 보는 것보다는 더 좋은 결과를 얻을 수 있음을 보였습니다. 이는 더 작은 PatchGAN은 더 적은 parameter를 가지고 더 빠르며 더 큰 이미지에 적용하는 데에서도 이점이 있음을 보여줍니다.

$D$는 이미지를 patch 크기 이상으로 분리된 픽셀 간의 독립성을 가정하여 Markov random field로 효과적으로 모델링합니다. 즉 PatchGAN은 texture loss / style loss로 해석할 수 있습니다.

2.2.3 Optimization and inference

일반적인 GAN의 접근법과 같습니다. 기존 GAN에서는 $log(1-D(x,G(x,z)))$를 최소화하는 대신 $logD(x,G(x,z))$를 최대화하는 것이 낫다고 봤습니다. 하지만 이 논문에서는 $D$를 최적화하는 목적 함수를 2로 나누어 $D$가 $G$보다 상대적으로 더 빠르게 학습되지 않도록 했습니다.

그 밖에는 minibatch SGD와 Adam을 사용했으며 batch size는 실험에 따라 1~10으로 조정하였습니다.

3. Experiments

Figure 3. Different losses induce different quality of results

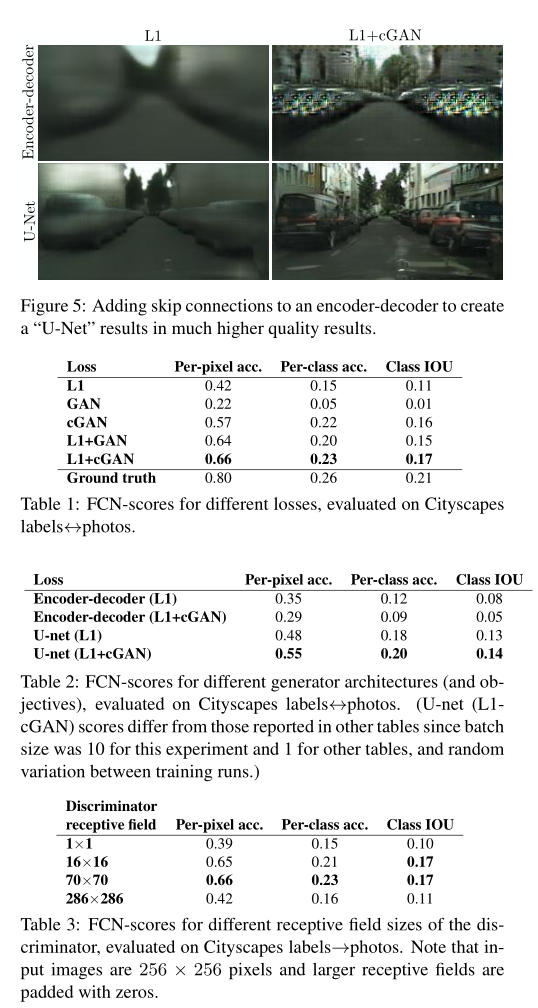
Figure 4. Adding skip connections to an encoder-decoder

Figure 5. Colorization results

Figure 6. Semantic segmentation

실험 결과에 대한 자세한 설명은 논문을 참고해주세요.

4. Conclusion

image-to-image translation 문제에 대해, 특히 고도로 구조화 된 그래픽 결과에 대해 conditional adversarial networks가 좋은 접근법이라는 것을 밝혔습니다. 이 네트워크는 문제와 데이터에 대한 손실을 학슴함으로써 넓은 범위의 문제에 대해 적합합니다.