[Paper Review] Neural transformation learning for deep anomaly detection beyond images
Reference
Neural transformation learning for deep anomaly detection beyond images
Qiu, C., Pfrommer, T., Kloft, M., Mandt, S., & Rudolph, M
International Conference on Machine Learning (2022)
https://proceedings.mlr.press/v139/qiu21a.html
Motivation
대조학습 등의 자기지도학습에서는 , 특히 이미지를 다룰 때에는 데이터 변환 (rotation, reflection, cropping, …)이 매우 중요한 역할을 합니다. 이렇게 데이터를 여러 형태로 변환한 뒤 이를 통해 의미 있는 표현 학습이 가능하며, 이렇게 학습된 표현은 이상 탐지 등의 테스크에도 유용하게 사용됩니다.
하지만 이미지가 아닌 다른 형태의 데이터, 특히 테이블 형태의 데이터나 시계열 데이터에는 이러한 데이터 변환을 적용하기 어렵습니다. 따라서 이러한 형태의 데이터에 적용 할 데이터 변환 기법에 대한 연구가 필요합니다. 이 논문에서는 학습 가능한 변환을 통한 end-to-end 이상 탐지 방법론을 제안합니다. 수동으로 데이터 변환 기법을 설계하기보다는, 하나의 목적 함수를 통해 유용한 데이터 변환 기법 및 이상 임계치를 함께 학습하게 됩니다.
Proposed Method

Figure 1. NeuTraL AD is a end-to-end procedure for self-supervised anomaly detection with learnable neural transformations. Each sample is transformed by a set of learned transformations and then embedded into a semantic space. The transformations and the encoder are trained jointly on a contrastive objective, which is also used to score anomalies.
본 논문에서 제안되는 모델인 NeuTraL AD는 (1) 데이터의 transformation을 학습하는 learnable transformation과 (2) transform 된 데이터의 표현을 추출하는 Encoder로 이루어져 있습니다. 두 구성 요소들은 본 논문에서 제안하는 DCL(Deterministic contrastive loss)를 통해 학습됩니다. 이러한 구조를 통해 학습 단계에서는 인코더의 파라미터와 transformation을 최적화하고, 시험 단계에서는 이상 여부를 판단하게 됩니다.
Learnerble Data Transformations
Transformation 방법이 총 $K$개가 있다고 가정할 때, $T = {T_1, …, T_k}$에서의 각각의 transformation은 각자 역전파를 통해 학습 가능한 고유한 파라미터 $\theta$를 가집니다. 가령 transformation $T_k$는 $\theta_k$를 가지게 됩니다. 본 논문에서는 $T_k$를 위해 신경망 모델을 사용했습니다.
Deterministic Contrastive Loss (DCL)
NeuTraL AD의 핵심 요소는 DCL이라는 손실 함수입니다. DCL은 transformation $k$가 적용된 샘플 $x_k = T_k(x)$가 원본 샘플 $x$와 비슷하게 되도록 유도하면서, 같은 샘플에 다른 transformation $l$이 적용된 $x_l = T_l(x)$와는 닮지 않게 되도록 합니다. 이를 점수로 나타내면 다음과 같습니다.
\[h(x_k, x_l) = \exp(\text{sim}(f_\phi(T_k(x)), f_\phi(T_l(x)))/\tau)\]여기서 $\text{sim}(z, z’)$는 $z$와 $z’$의 코사인 유사도를 의미하며, $\tau$는 temperature 파라미터 입니다. 또한 $f_\phi(x)$는 $x$에서 feature를 뽑아내는 encoder (= feature extractor) 입니다. 즉 인코더가 $x_k$에서 뽑아낸 feature와 $x_l$에서 뽑아낸 feature가 유사할수록 점수가 높게 됩니다.
\[\mathcal{L} :=\mathbb{E}_{x \sim \mathcal{D}}\left[-\sum^K_{k=1}\log\frac{h(x_k, x)}{h(x_k, x) + \sum_{l\ne k}h(x_k, x_l)}\right]\]위 식은 DLC를 나타냅니다. 분자는 transformation 된 샘플에서 뽑힌 feature는 원본 샘플에서 뽑힌 feature와 가깝도록 유도합니다. 이를 통해 각 transformation들이 데이터의 중요한 정보들을 보존하도록 유도합니다. 동시에 분모는 transform된 모든 샘플들의 임베딩이 서로 멀어지도록 유도하며, 따라서 다양한 transformation이 만들어지도록 합니다. NeuTral AD의 파라미터 $\theta = [\phi, \theta_{1:K}]$는 인코더의 파라미터 $\phi$와 각 learnable transformation들의 파라미터 $\theta_{1:K}$이 있으며, 모든 파라미터들은 동시에 학습됩니다.
Anomaly Score
이 모델의 특징 중 하나는 위의 학습 손실이 곧 이상치 점수로도 기능한다는 점입니다. 이상치 점수는 다음과 같습니다.
\[S(x) = -\sum^K_{k=1}\log\frac{h(x_k, x)}{h(x_k, x) + \sum_{l\ne k}h(x_k, x_l)}\]다른 대조학습 기반의 이상 탐지 방법론은 대부분의 경우 이상치 점수의 계산을 위해 negative sample을 필요로 하지만, 본 방법론에서 제안하는 이상치 점수는 negative sample을 필요로 하지 않기 때문에 새로운 데이터 $x$에 대해 바로 이상치 점수를 도출 해낼 수 있습니다. DCL을 최소화함으로써 학습 데이터들의 이상치 점수를 최소화 할 수 있으며, 따라서 이상치 점수가 높을수록 학습 데이터와 거리가 먼 데이터라고 볼 수 있습니다.
A Theory of Neural Transformation Learning
해당 논문에서는 위에서 제안된 방법의 이론적 근거를 설명하고 있습니다. 우선 self-supervised 이상 탐지를 위한 transformation의 학습을 위해서는 다음과 같은 조건을 만족해야 합니다.
- Semantics : Transformation 된 샘플들은 원본 샘플과 의미적인 정보를 공유해야 합니다.
- Diversity : Transformation는 원본 샘플에 다양한 view를 제공해야 합니다.
기존에 선행 연구에서 제안된 손실 함수들로는 위 조건들을 만족시키는 Transformation의 학습이 잘 이루어지지 않습니다. 이를 설명하기 위해서 두 가지의 극단적인 케이스를 가정합니다.
- Constant transformation : $T_k(x) = c_k$로, 입력된 샘플과 상관없이 항상 같은 결과를 출력합니다.
- Identitiy transformation : $T_1(x) = … = T_k(x) = x$ 로 모든 Transformation 들이 항상 입력된 샘플을 그대로 출력합니다.
가령 어떤 Transformation인지 예측하는 손실 함수가 있는데, 이 경우 1번과 같은 constant transformation일 경우 어떤 transformation이 적용 되었는지 예측하는 것이 매우 쉬워집니다. 또한 SimCLR의 손실 함수의 경우 Positive 쌍을 찾는 것을 목적으로 하는데, 2번과 같은 Identity transformation이 된 경우 문제가 매우 쉽게 풀리게 됩니다. 이처럼 기존에 제안된 연구들에서 사용된 손실 함수를 그대로 사용 할 경우 본 논문에서 제안하는 Neural Transformation은 Semantics 혹은 Diversity의 조건을 만족하지 않는 방향으로 학습 될 가능성이 큽니다. 더해서 손실값이 입력된 샘플이 정상인지 이상인지와 상관 없어지게 됩니다. DCL의 경우, 분자에서 Semantic을, 분모에서 Diversity를 만족하도록 학습하며, 동시에 입력된 샘플이 정상인지 이상인지에 따라 점수가 나타나게 됩니다.
Experiments
본 논문에서 제안하는 NeuTraL AD는 image가 아닌 다른 도메인의 데이터를 위한 이상 탐지를 목적으로 합니다.
Evaluation Protocol
크게 두가지 방식이 사용됩니다.
- one-vs-rest. : $N$개의 클래스가 존재하는 데이터에서 각각의 클래스를 정상, 나머지 클래스를 이상으로 보는 one class classification task를 수행하며, 학습 단계에선 정상 클래스만 사용되고 시험 단계에선 모든 클래스를 대상으로 합니다.
- n-vs-rest. : 위와 같으나, 1개의 클래스가 아닌 $1 < n < N$의 $n$개 클래스를 정상으로 보고 나머지를 이상으로 봅니다. 나머지는 같습니다. 더 어려운 task입니다.
Anomaly Detection of Time Series
여기서 시계열 데이터를 대상으로 한 목표는, 전체 시퀀스 레벨에서 이상 시계열을 발견하는 것입니다. 어떤 시점에 이상인지 파악할 수 있는 것은 아니며 분류 문제로 접근했다고 볼 수 있습니다. 이때 Transformation $T_k$는 3개의 1D CNN의 Residual Block 층으로 구성되어 있는 모델 $M_k(x)$에 $x$를 elementwise multiplication 한 $M_k(x) * x$을 사용했습니다. 결과는 다음과 같습니다.

Table 1. Average AUC with standard deviation for one-vs-rest anomaly detection on time series datasets.
대부분의 데이터에서 뛰어난 성능을 보였으며, 특히 random transformation을 사용한 self-supervised learning 방법인 GOAD에 비해 뛰어난 성능을 보이고 있습니다. fixed Ts의 경우 12가지의 적절한 Transformation 방법으로 고정 시킨 것인데, 더 많은 경우 뛰어난 성능을 보였으므로 learned transformation의 효과를 알 수 있는 결과입니다.

Figure 2. NeuTraL AD is a end-to-end procedure for self-supervised anomaly detection with learnable neural transformations. Each sample is transformed by a set of learned transformations and then embedded into a semantic space. The transformations and the encoder are trained jointly on a contrastive objective, which is also used to score anomalies.
위 그림은 SAD 데이터셋에 대해 학습 전후의 anomaly score를 나타낸 것으로 이상치들을 뚜렷하게 구분하고 있다는 점을 알 수 있습니다.

Figure 3. 3D visualization (projected using PCA) of how the original samples (blue) from the SAD dataset and the different views created by the neural transformations of NeuTraL AD (one color per transformation type) cluster in data space (Figures 3a and 3b) and in the embedding space of the encoder (Figures 3c and 3d).
위 그림은 SAD 데이터셋에 $K=4$인 transformation을 적용해서 PCA로 시각화 한 결과입니다. 밑의 (c)와 (d)의 경우 인코더를 통해 추출한 결과인데, 정상 데이터의 경우 transformation에 따라 매우 잘 모여있는 반면 이상 데이터의 경우 군집이 전혀 이루어지지 않고 있는 점을 확인 할 수 있습니다. 위와 같이 학습되기 때문에 이상 탐지가 잘 이루어지게 됩니다.

Table 2. Average AUC with standard deviation for n-vs-rest (n = N − 1) anomaly detection on time series datasets.

Figure 4. AUC result of n-vs-all experiments on SAD and NATOPS with error bars (barely visible due to significance). NeuTraL AD outperforms all baselines on NATOPS and all deep learning baselines on SAD. LOF, a method based on k-nearest neighbors, outperforms NeuTraL AD, when n > 3 on SAD.
정상 클래스에 속하는 클래스가 늘어남에 따라 정상 데이터의 분산이 커지게 되고, 모든 모델들의 성능이 떨어지게 됩니다. 특히 딥러닝 기반의 방법들이 성능 하락 폭이 큰 모습을 볼 수 있습니다. 본 논문에서 제안하는 방법론의 경우에도 성능 하락이 눈에 띄지만, 다른 딥러닝 기반 방법들에 비해서는 뛰어난 성능을 보여주고 있습니다.
Anomaly Detection of Tabular Data
여기서는 Transformation $T_k$는 3개의 Dense Layer로 구성된 MLP $M_k(x) * x$ 입니다. 마찬가지로 데이터셋에 따라 $K$는 다르게 설정 되었습니다.

Table 3. F1-score (%) with standard deviation for anomaly detection on tabular datasets (choice of F1-score consistent with prior work).
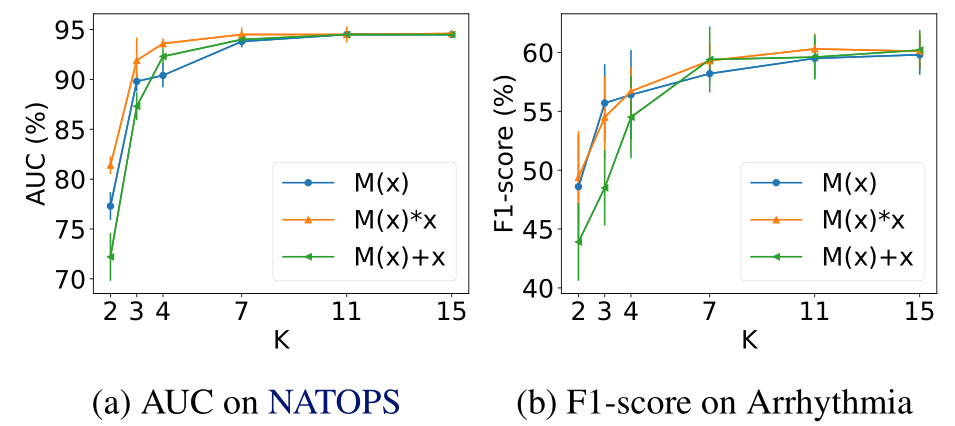
Figure 5. The outlier detection accuracy in terms of AUC of NeuTraL AD on NATOPS and in terms of F1-score of NeuTraLAD on Arrhythmia increases as the number of transformations K increases, but stabilizes when a certain threshold is reached (K >≈ 10). With enough transformations, NeuTraL AD is robustto the parametrization of the transformations.
성능이 좋았습니다. 또한 $T_k$에 다른 여러가지 방법도 사용해보았는데, $K > 4$인 경우 거의 차이가 없었으며, $K \le 4$인 경우 학습 된 transformation이 이상 탐지에 의미있는 정보를 제공하는 것이 확실치 않으므로 비교적 떨어지는 성능을 보였습니다.

댓글남기기